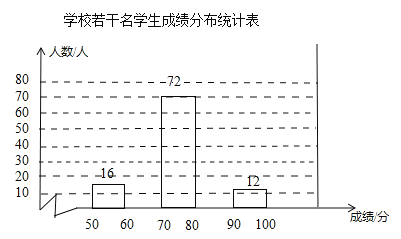
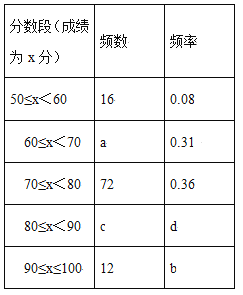
题目内容
【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab+2ab+a. 如:13=1×3+2×1×3+1=16
(1)求3(﹣1)的值;
(2)若(a+1)2=36,求a的值;
(3)若m=2x,n=(![]() x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小.
【答案】(1)0,(2)a=3,(3)m>n.
【解析】
(1)根据运算的定义展开即可解题,
(2)根据运算的定义展开左侧,构成一次方程,求解方程即可,
(3)根据运算的定义展开求出m,n,利用作差法表示出m-n=2x+2,最后根据非负性即可解题.
解:(1)由题可知, 3(﹣1)=3-6+3=0,
(2)(a+1)×4+4(a+1)+(a+1)=36,
整理得9(a+1)=36
解得a=3,
(3)m=2x=2x+4x+2, n=(![]() x)3=
x)3=![]() x+
x+![]() x+
x+![]() x =4x,
x =4x,
∴m-n=2x+2>0,
∴m>n.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目