题目内容
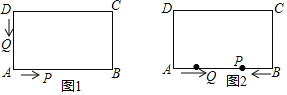
【题目】如图1,在长方形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
(1)如图1,当点P到达点B,或点Q到达点A时,两点都停止运动.
①当t=3时,分别求AQ和BP的长;
②当t为何值时,线段AQ与线段AP相等?
(2)如图2,若P,Q到达B,A后速度不变继续运动,点Q开始向点B移动,P点返回向点A移动,其中一点到达目标点后就停止运动.问当t为何值时,线段PQ的长度等于线段BC长度的一半.
【答案】(1)①AQ=3cm,BP=6cm,②t=2s时,AQ=AP;(2)当t=3s或5s时,线段PQ的长度等于线段BC长度的一半
【解析】
(1)①根据AQ=AD-DQ,BP=AB﹣AP计算即可;
②构建方程即可解决问题;
(2)分相遇前,相遇后两种情形构建方程即可;
解:(1)①当t=3时,AQ=AD﹣DQ=6﹣3×1=3cm,
BP=AB﹣AP=12﹣3×2=6cm.
②当AQ=AP时,6﹣t=12﹣2t,
解得t=2s.
∴t=2s时,AQ=AP.
(2)相遇前,由题意可得:12﹣t﹣2t=![]() ×6,
×6,
解得t=3.
相遇后,由题意:3t﹣12=![]() ×6,
×6,
解得t=5,
综上所述,当t=3s或5s时,线段PQ的长度等于线段BC长度的一半.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目