题目内容
（2013•燕山区一模）定义：对于平面直角坐标系中的任意线段AB及点P，任取线段AB上一点Q，线段PQ长度的最小值称为点P到线段AB的距离，记作d（P→AB）．
已知O为坐标原点，A（4，0），B（3，3），C（m，n），D（m+4，n）是平面直角坐标系中四点．根据上述定义，解答下列问题：
（1）点A到线段OB的距离d（A→OB）=
（2）已知点G到线段OB的距离d（G→OB）=
，且点G的横坐标为1，则点G的纵坐标为
（3）当m的值变化时，点A到动线段CD的距离d （A→CD）始终为2，线段CD的中点为M．
①在图（2）中画出点M随线段CD运动所围成的图形并求出该图形的面积．
②点E的坐标为（0，2），m＞0，n＞0，作MH⊥x轴，垂足为H．是否存在m的值，使得以A、M、H为顶点的三角形与△AOE相似？若存在，求出m的值；若不存在，请说明理由．
已知O为坐标原点，A（4，0），B（3，3），C（m，n），D（m+4，n）是平面直角坐标系中四点．根据上述定义，解答下列问题：
（1）点A到线段OB的距离d（A→OB）=
2
| 2 |
2
；| 2 |
（2）已知点G到线段OB的距离d（G→OB）=
| 5 |
1-
或1+
| 10 |
| 10 |
1-
或1+
．| 10 |
| 10 |
（3）当m的值变化时，点A到动线段CD的距离d （A→CD）始终为2，线段CD的中点为M．
①在图（2）中画出点M随线段CD运动所围成的图形并求出该图形的面积．
②点E的坐标为（0，2），m＞0，n＞0，作MH⊥x轴，垂足为H．是否存在m的值，使得以A、M、H为顶点的三角形与△AOE相似？若存在，求出m的值；若不存在，请说明理由．
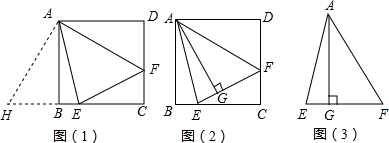
分析：（1）如图（1）过点A作AC⊥OB于C，由B点的坐标就可以得出OB平分∠xOy，由勾股定理就可以求出AC的值而得出结论；
（2）如图（2），过点G1作G1F⊥OB于点F，则G1F就是点G1到线段OB的距离．过点D作G2D⊥OB交直线x=1于点G2，由直角三角形的性质和勾股定理就可以求出结论；
（3）①如图（3），运用分类讨论思想，当点C在以A为圆心，半径为2的⊙A的右半圆上时，当点C从C1到C2时，当点C从C4到C3时，当点D在以A为圆心，半径为2的⊙A的左半圆上时，点M在圆弧M1FM4上运动；根据圆的面积公式和矩形的面积公式就可以求出结论；
②利用分类思想分情况讨论如图（4），当点M位于左侧圆弧上时，m≤0，不合题意；如图（4），当点M位于线段M1M2上时，由学生三角形的性质就可以求出结论，如图（5），当点M位于右侧圆弧M1FM4上时，连结GM，其中点G是圆弧的圆心，坐标为（6，0）．根据勾股定理建立方程就可以求出结论．
（2）如图（2），过点G1作G1F⊥OB于点F，则G1F就是点G1到线段OB的距离．过点D作G2D⊥OB交直线x=1于点G2，由直角三角形的性质和勾股定理就可以求出结论；
（3）①如图（3），运用分类讨论思想，当点C在以A为圆心，半径为2的⊙A的右半圆上时，当点C从C1到C2时，当点C从C4到C3时，当点D在以A为圆心，半径为2的⊙A的左半圆上时，点M在圆弧M1FM4上运动；根据圆的面积公式和矩形的面积公式就可以求出结论；
②利用分类思想分情况讨论如图（4），当点M位于左侧圆弧上时，m≤0，不合题意；如图（4），当点M位于线段M1M2上时，由学生三角形的性质就可以求出结论，如图（5），当点M位于右侧圆弧M1FM4上时，连结GM，其中点G是圆弧的圆心，坐标为（6，0）．根据勾股定理建立方程就可以求出结论．
解答：解：（1）作AC⊥OB于C，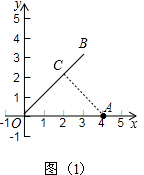
∴∠ACO=90°．
∵B（3，3），
∴OB平分∠xOy，
∴∠AOB=45°．
∴∠OAC=45°，
∴∠OAC=∠AOC，
∴AC=OC．
∵A（4，0），
∴OA=4．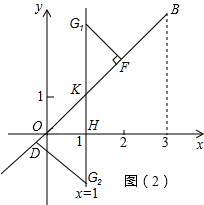
在Rt△AOC中，由勾股定理，得
AC=2
．
∴点A到线段OB的距离d（A→OB）=2
．
故答案为：2
；
（2）∵OB平分∠xOy，
∴OB的解析式为：y=x
∵点G的横坐标为1，
∴点G在直线x=1上，设直线x=1交x轴于点H，交OB于点K．
①如图，过点G1作G1F⊥OB于点F，则G1F就是点G1到线段OB的距离．
∵OB的解析式为：y=x，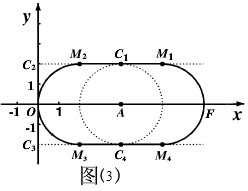
∴△G1FK，△DHK均为等腰直角三角形，
∵d（G1→OB）=
，
∴KF=
，由勾股定理得GK=
，
∵KH=OH=1，
∴HG1=
+1．
即G1的纵坐标为
+1；
②如图，过点D作G2D⊥OB交直线x=1于点G2，由题意知△DKG2为等腰直角三角形，
∵d（G2→OB）=
，
∴DK=DG2=
，
∴G2K=
．
∴G2H=
-1
∴点G2同样是满足条件的点．
∴点G2的纵坐标为1-
．
综上，点G的纵坐标为1+
或1-
．
（3）①如图（3），当点C在以A为圆心，半径为2的⊙A的右半圆上时，点M在圆弧M1FM4上运动；
当点C从C1到C2时，点M在线段M1M2上运动；
当点C从C4到C3时，点M在线段M4M3上运动；
当点D在以A为圆心，半径为2的⊙A的左半圆上时，点M在圆弧M2OM3上运动；
∴点M随线段CD运动所围成的封闭图形是图中实线部分，面积为16+4π．
②存在．
图（4）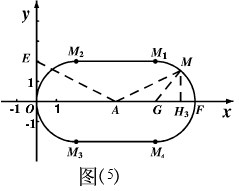
由A（4，0），E（0，2），得
=
=
．
（ i）当点M位于左侧圆弧上时，m≤0，不合题意；
（ ii）如图（4），当点M位于线段M1M2上时，
∵MH=2，∴只要AH=1，就有△AOE∽△MHA，
此时OH1=5，OH2=3．
∵点M为线段CD的中点，CD=4，
∴OH1=5时，m=3；OH2=3时，m=1．
（ iii）如图（5），当点M位于右侧圆弧M1FM4上时，连结GM，其中点G是圆弧的圆心，坐标为（6，0）．
图（5）设MH3=x，∵AH3＞M3H3
∴AH3=2x，∴GH3=2x-2，又GM=2，
在Rt△MGH3中，由勾股定理得：（2x-2）2+x2=22，
解得x1=
，x2=0（不合题意，舍去），
此时AH3=
，OH3=OA+AH3=
，
∵点M为线段CD的中点，CD=4，∴m=
．
综上所述，存在m=1或m=3或m=
，使得以A、M、H为顶点的三角形与△AOD相似．
∴∠ACO=90°．
∵B（3，3），
∴OB平分∠xOy，
∴∠AOB=45°．
∴∠OAC=45°，
∴∠OAC=∠AOC，
∴AC=OC．
∵A（4，0），
∴OA=4．
在Rt△AOC中，由勾股定理，得
AC=2
| 2 |
∴点A到线段OB的距离d（A→OB）=2
| 2 |
故答案为：2
| 2 |
（2）∵OB平分∠xOy，
∴OB的解析式为：y=x
∵点G的横坐标为1，
∴点G在直线x=1上，设直线x=1交x轴于点H，交OB于点K．
①如图，过点G1作G1F⊥OB于点F，则G1F就是点G1到线段OB的距离．
∵OB的解析式为：y=x，
∴△G1FK，△DHK均为等腰直角三角形，
∵d（G1→OB）=
| 5 |
∴KF=
| 5 |
| 10 |
∵KH=OH=1，
∴HG1=
| 10 |
即G1的纵坐标为
| 10 |
②如图，过点D作G2D⊥OB交直线x=1于点G2，由题意知△DKG2为等腰直角三角形，
∵d（G2→OB）=
| 5 |
∴DK=DG2=
| 5 |
∴G2K=
| 10 |
∴G2H=
| 10 |
∴点G2同样是满足条件的点．
∴点G2的纵坐标为1-
| 10 |
综上，点G的纵坐标为1+
| 10 |
| 10 |
（3）①如图（3），当点C在以A为圆心，半径为2的⊙A的右半圆上时，点M在圆弧M1FM4上运动；
当点C从C1到C2时，点M在线段M1M2上运动；
当点C从C4到C3时，点M在线段M4M3上运动；
当点D在以A为圆心，半径为2的⊙A的左半圆上时，点M在圆弧M2OM3上运动；
∴点M随线段CD运动所围成的封闭图形是图中实线部分，面积为16+4π．
②存在．
图（4）
由A（4，0），E（0，2），得| OE |
| OA |
| 2 |
| 4 |
| 1 |
| 2 |
（ i）当点M位于左侧圆弧上时，m≤0，不合题意；
（ ii）如图（4），当点M位于线段M1M2上时，
∵MH=2，∴只要AH=1，就有△AOE∽△MHA，
此时OH1=5，OH2=3．
∵点M为线段CD的中点，CD=4，
∴OH1=5时，m=3；OH2=3时，m=1．
（ iii）如图（5），当点M位于右侧圆弧M1FM4上时，连结GM，其中点G是圆弧的圆心，坐标为（6，0）．
图（5）设MH3=x，∵AH3＞M3H3
∴AH3=2x，∴GH3=2x-2，又GM=2，
在Rt△MGH3中，由勾股定理得：（2x-2）2+x2=22，
解得x1=
| 8 |
| 5 |
此时AH3=
| 16 |
| 5 |
| 36 |
| 5 |
∵点M为线段CD的中点，CD=4，∴m=
| 26 |
| 5 |
综上所述，存在m=1或m=3或m=
| 26 |
| 5 |
点评：本题考查了点到直线的距离的运用，等腰直角三角形的性质的运用，勾股定理的运用，相似三角形的判定及性质的运用，点的坐标的运用，解答时证明三角形相似由相似三角形的性质求解是关键．
练习册系列答案
相关题目
（2013•燕山区一模）如图，点P是⊙O的弦AB上任一点（与A，B均不重合），点C在⊙O上，PC⊥OP，已知AB=8，设BP=x，PC2=y，y与x之间的函数图象大致是（ ）
（2013•燕山区一模）如图，直线y=2x-1与反比例函数