��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�ֱ�� ��������y��ax2��bx��3��a��0������A��B���㣬��A��x���ϣ���B��������Ϊ5����P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D��
��������y��ax2��bx��3��a��0������A��B���㣬��A��x���ϣ���B��������Ϊ5����P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D��
��1���������ߵĽ���ʽ��
��2�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij���������߶�PD�������ֵ��
������PB���߶�PC�ѡ�PDB�ֳ����������Σ��Ƿ�����ʺϵ�m��ֵ��ʹ�����������ε������Ϊ1:2�������ڣ�ֱ��д��m��ֵ���������ڣ���˵�����ɣ�
��1��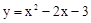 ����2����
����2����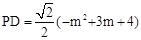 ��
��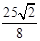 ����0��3.
����0��3.
���������������1����y=x+1�У���y=0ʱ��x=-1����y=5ʱ��x=4�����˿ɵ�A��B�����ꣻ��A��B������������߽���ʽ���a��b��ֵ������ȷ���������߽���ʽ��
��2������ֱ��AB��y�ύ�ڵ�E����CP��y��ƽ�У��õ���ACP=��AEO�����AE��OA�ij����ó�sin��AEO��ֵ����Ϊsin��ACP��ֵ����P�ĺ�����Ϊm���ֱ����ֱ���������߽���ʽ�õ�����������֮��ΪPC�ij�����PD=PCsin��ACP��ʾ��PD�����ö��κ������������PD�����ֵ���ɣ�
�ڴ��ڣ���D��DF��CP����B��BG��PQ����PC�ӳ������Q����ʾ��DF��BG��������ʾ��������DCP�����������BCP������������֮��Ϊ1��2�г�����m�ķ��̣�������̵Ľ�õ�m��ֵ���ɣ�
�����������1����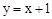 �У���y=0ʱ��x=-1����y=5ʱ��x=4��
�У���y=0ʱ��x=-1����y=5ʱ��x=4��
��A(-1��0)��B(4��5) .
��A(-1��0)��B(4��5)�ֱ����y��ax2��bx��3�У���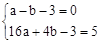 �����
�����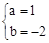 ��
��
���������ʽΪ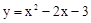 .
.
��2������ֱ��AB��y���ڵ�E�����E��0��1������OA=OE����AEO=45��,��ACP=��AEO="45��,"
��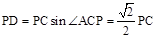 ��
��
��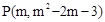 ����
����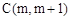 ��
��
��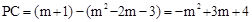 ��
��
��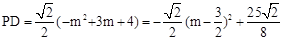 ��
��
��PD�����ֵΪ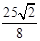 ��
��
�ڵ�m=0��m=3ʱ��PC�ѡ�PDB�ֳ����������ε������Ϊ1:2��
��ͼ����D��DF��CP����B��BG��PQ����PC�ӳ������Q��
��sin��ACP=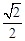 ����cos��ACP=
����cos��ACP=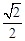 .
.
��Rt��PDF�У�DF=DP•sin��DPC=DP•cos��ACP=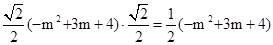 .
.
�֡�BG=4-m��
��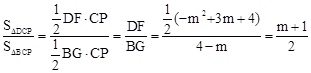 .
.
��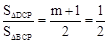 ʱ����ã�m=0��
ʱ����ã�m=0��
�� 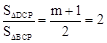 2ʱ����ã�m=3��
2ʱ����ã�m=3��
�ʵ�m=0��m=3ʱ��PC�ѡ�PDB�ֳ����������ε������Ϊ1��2��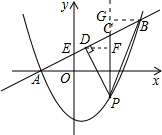
���㣺1.���κ����ۺ��⣻2.����ϵ������������ʽ��3.������ͼ�����ʣ�4.���κ�����ͼ�������ʣ�5.������Ǻ������壻6.�����ε������7.����˼���Ӧ��.

 һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д� ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �У����κ���
�У����κ��� ��ͼ����
��ͼ���� �ύ�ڵ�A��B����B�ڵ�A����ࣩ����
�ύ�ڵ�A��B����B�ڵ�A����ࣩ���� �ύ�ڵ�C��������H��0,
�ύ�ڵ�C��������H��0,  ����ƽ����
����ƽ���� ����DEΪֱ������Q������Q��
����DEΪֱ������Q������Q��

 ������A��3��2����B��0��1���͵�C
������A��3��2����B��0��1���͵�C ��
�� �����F�����ꣻ
�����F�����ꣻ

 ��ͼ����x��������ύ��A
��ͼ����x��������ύ��A ��B
��B ���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C ����A�͵�B��ľ���Ϊ2�� �������κ���
���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C ����A�͵�B��ľ���Ϊ2�� �������κ��� �������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
 �ϵ�һ�����㣬�ҵ�A�ڵ�һ�����ڣ�AE��y���ڵ�E����B����Ϊ(O��2)��ֱ��AB��
�ϵ�һ�����㣬�ҵ�A�ڵ�һ�����ڣ�AE��y���ڵ�E����B����Ϊ(O��2)��ֱ��AB�� ���ڵ�C����D���C����y��Գƣ�ֱ��DE��AB�ཻ�ڵ�F������BD�����߶�AE�ij�Ϊm����BED�����ΪS��
���ڵ�C����D���C����y��Գƣ�ֱ��DE��AB�ཻ�ڵ�F������BD�����߶�AE�ij�Ϊm����BED�����ΪS�� ʱ����S��ֵ��
ʱ����S��ֵ�� �ĺ�������ʽ��
�ĺ�������ʽ�� ʱ����
ʱ���� ��ֵ��
��ֵ�� ������k��m��������ϵ��֤����
������k��m��������ϵ��֤����
