Question

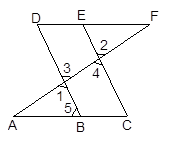
将含300角的三角板ABC如图放置，使其三个顶点分别落在三条平行直线上，其中∠ACB=900，当∠1=600时，图中等于300的角的个数是（    ）

A．6个

B．5个

C．4个

D．3个

Answer 1

B

专题：推理填空题．
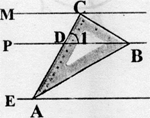
分析：在△CDB中，根据∠ACB=90°，∠1=60°求得∠CBD=30°，然后由平行线的性质找30°的角；在△ABC中，∠ACB=90°，∠A=30°，求得∠CBA=60°，∠DBA=∠CBA-∠CBD=30°，然后再由两直线平行，内错角相等，找30°的角．
解答：解：在△CDB中，∠ACB=90°，∠1=60°，
∴∠CBD=30°；
∵MC∥PB，
∴∠ECB=∠CBD=30°（两直线平行，内错角相等）；
在△ABC中，∠ACB=90°，∠A=30°，
∴∠CBA=60°，
∠DBA=∠CBA-∠CBD=30°；
∵PB∥EF，
∴∠BAF=∠DBA=30°（两直线平行，内错角相等）；
∴符合题意的角有5个．
故选B．
点评：本题考查了平行线的性质．解答本题时，主要利用了直角三角形的两个锐角互余、两直线平行，内错角相等的知识．