题目内容
【题目】在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，如图，已知点A（0，1），B（2，0），请在所给网格区域（含边界）上，按要求找到整点．
（1）画一个直角三角形ABC，使整点C的横坐标与纵坐标相等；
（2）若△PAB（不与△ABC重合）的面积等于△OAB的面积，则符合条件点整P共有 个．
【答案】（1）见解析；（2）3
【解析】
（1）由题意利用数形结合的思想进行分析解决问题即可；
（2）根据题意利用三角形面积公式分析，可知满足条件的点P有3个．
解：（1）C点坐标为（4，4）．
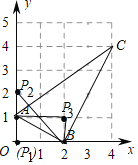
（2）
，要使△PAB（不与△ABC重合）的面积也为1，
只需要满足底和高的乘积为2，且点P为整数点，
可知满足条件的点P有3个，如上图所示，分别为
.
故答案为：3．
练习册系列答案
相关题目
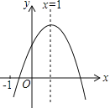
【题目】己知二次函数y=ax2+bx+c的y与x的部分对应值如下表；
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论：①抛物线的开口向下；②其图象的对称轴为x=1;③当x﹤l时，函数值y随x 的增大而增大；④方程ax2+bx+c=0有一个根大于4.其中正确的结论有（ ）
A. 4个B. 1个C. 3个D. 2个
