题目内容
【题目】如图，等腰直角三角形ABC中，∠C=90°，点D是△ABC的重心，以AD为直角边作等腰Rt△ADE，若△ABC的周长为6，则△ADE的周长为__________．
【答案】
【解析】
如图，延长AD交BC于点F，在直角OACF中，利用勾股定理求得AF的长度，然后由重心的性质求得AD的长度，结合等腰直角三角形的性质即可求得△ADE的周长；
解：∵等腰直角三角形ABC中，∠C=90°，
∴AC=BC，
，
∴
，
又∵△ABC的周长为6，
∴
，则
，
如图，延长AD交BC于点F，
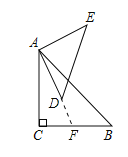
∵点D是△ABC的重心，
∴CF=
，即CF=
，
在直角△ACF中，由勾股定理得，
=
；
则AD=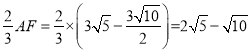
，
∴在等腰Rt△ADE中，
，
，
∴△ADE的周长=AD+DE+AE=
；
故答案为：；
练习册系列答案
阅读快车系列答案
相关题目
