题目内容
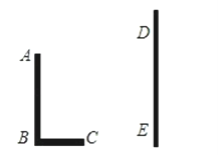
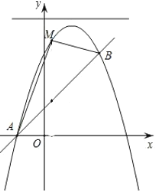
【题目】如图所示，是由北京国际数学家大会的会徽演化而成的图案，其主体部分是由一连串的等腰直角三角形依次连接而成，其中∠MA1A2＝∠MA2A3…＝∠MAnAn+1＝90°，（n为正整数），若M点的坐标是（﹣1，2），A1的坐标是（0，2），则A22的坐标为（ ）
A.（﹣1﹣29，2﹣29）B.（1﹣29，2﹣29）
C.（﹣1﹣210，2﹣210）D.（1﹣210，2﹣210）
【答案】C
【解析】
根据题意观察并探究规律，利用规律解决问题即可．
解：观察图象可知，点的位置是8个点一个循环，
∴A22与A6，A14的位置都在第三象限，且在直线y＝x+3上，
∵第一个等腰直角三角形的直角边为1，第二个等腰直角三角形的边长为
，…，第n个等腰直角三角形的边长为（）n-1，
∴第22个等腰直角三角形的边长为（）21，可得A22M＝（）21，
直角边长为
，
∴A22（﹣1﹣210，2﹣210），
故选：C．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
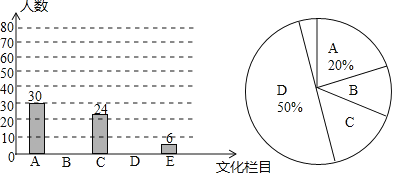
【题目】某校为了解学生的课外阅读情况，随机调查了部分学生平均每天的课外阅读时间，并根据调查结果制成被调查学生人数的统计图表如下，但信息不完整．
时间(小时) | 0.5 | 1 | 1.5 | 2 |
人数 | 2 | 5 | 3 |
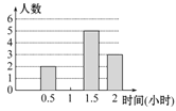
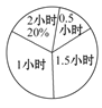
请根据所提供信息，解决下列问题：
（1）求扇形统计图中，读书时间为“2小时”部分的圆心角的度数．
（2）通过计算估计全校每个学生平均每天的课外阅读时间．
（3）从被调查的课外读书时间最少和最多的学生中，随机抽2个学生进行访谈，求各抽到1人的概率．
