题目内容
如图,在四边形ABCD中,∠ABC=90°,AB=3 ,BC=
,BC= ,DC=12,AD=13,求四边形ABCD的面积.
,DC=12,AD=13,求四边形ABCD的面积.
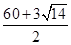 .
.
解析试题分析:连接AC,先根据勾股定理求出AC的长,再勾股定理的逆定理可证△DCA为直角三角形,然后将两个直角三角形的面积相加即为四边形ABCD的面积.
连接AC,
∵AB=3 ,BC=
,BC= ,∠ABC=90°,∴
,∠ABC=90°,∴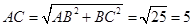 .
.
∵DC=12,AD=13,∴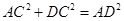 .∴△DCA为直角三角形.
.∴△DCA为直角三角形.
∴四边形ABCD的面积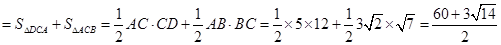 .
.
答:四边形ABCD的面积为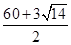 .
.
考点:勾股定理和逆定理.

练习册系列答案
相关题目
如图,在△ABC中,DE∥BC,若AD:AB=1:3,则△ADE与△ABC的面积之比是
| A.1:3 | B.1:4 | C.1:9 | D.1:16 |
在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S四边形ABCE为( )
| A.3:4 | B.4:3 | C.7:9 | D.9:7 |
如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a= b b | B.a=2b | C.a=2 b b | D.a=4b |

 ∠2,∠1+∠2=162°,求∠3与∠4的度数.
∠2,∠1+∠2=162°,求∠3与∠4的度数.

 、
、 被
被 、
、 所截,且
所截,且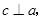

 ,求∠3的大小.
,求∠3的大小.