题目内容
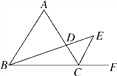
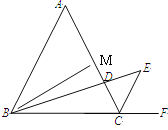
【题目】如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
【答案】(1)详见解析;(2)3![]() .
.
【解析】试题分析:(1)根据等边三角形的性质可得∠BAC=∠ACB=60°,∠ACF=120°,再根据角平分线的性质可得∠ACE=60°,再结合对顶角∠ADB=∠CDE,即可证得结果;
(2)作BM⊥AC于点M,根据等边三角形的性质可得AM=CM=3,BM=AB·sin60°=![]() ,由AD=2CD可得CD=2,AD=4,MD=1,在Rt△BDM中,根据勾股定理可求得BD的长,再根据△ABD∽△CED结合相似三角形的性质可求的ED的长,即可求得结果.
,由AD=2CD可得CD=2,AD=4,MD=1,在Rt△BDM中,根据勾股定理可求得BD的长,再根据△ABD∽△CED结合相似三角形的性质可求的ED的长,即可求得结果.
(1)∵△ABC是等边三角形
∴∠BAC=∠ACB=60°,∠ACF=120°
∵CE是外角平分线
∴∠ACE=60°
∴∠BAC=∠ACE
又∵∠ADB=∠CDE
∴△ABD∽△CED;
(2)作BM⊥AC于点M,AC=AB=6
∴AM=CM=3,BM=AB·sin60°=![]()
∵AD=2CD,
∴CD=2,AD=4,MD=1
在Rt△BDM中,BD=![]() =
=![]()
由(1)△ABD∽△CED得, ![]() ,
, ![]() ,
,
∴ED=![]() ,
,
∴BE=BD+ED=![]() .
.

练习册系列答案
相关题目