题目内容
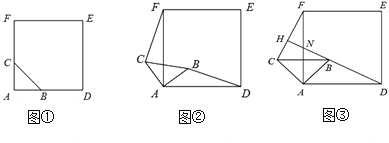
【题目】如下图,![]() 和
和![]() 是等腰直接角三角形,
是等腰直接角三角形,![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 恰好是
恰好是![]() 中点,连接
中点,连接![]() .
.
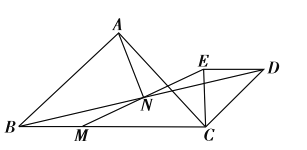
(1)求证:![]() ;
;
(2)连接AM、AE,请探究AN与EN的位置关系与数量关系。
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.
【答案】(1)见解析;(2)①AN⊥EM,AN=![]() EM;②见解析;
EM;②见解析;
【解析】
(1)由∠CED=∠BCE=90°,可证得BC∥DE,然后由点N恰好是BD中点,利用ASA可证得△BMN≌△DEN,继而证得结论;
(2)首先连接AM,AE,由△ABC和△CDE是等腰直角三角形,易证得△ABM≌△ACE,则可证得△AME是等腰直角三角形,继而证得AN⊥EM,AN=![]() EM.
EM.
(1)证明:∵∠CED=∠BCE=90°,
∴BC∥DE,
∴∠MBN=∠EDN,
∵点N恰好是BD中点,
∴BN=DN,
在△BMN和△DEN中,
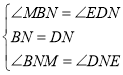 ,
,
∴△BMN≌△DEN(ASA),
∴MN=EN;
(2)①位置关系:AN⊥EM,数量关系:AN=![]() EM.
EM.
故答案为:AN⊥EM,AN=![]() EM.
EM.
②证明:连接AM,AE,
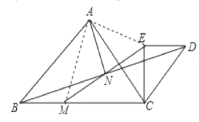
∵△BMN≌△DEN,
∴BM=DE,
∵△ABC和△CDE是等腰直角三角形,
∴AB=AC,∠ABM=∠ACB=45°,DE=CE,
∴BM=CE,
∵∠BCE=90°,
∴∠ACE=45°,
∴∠ABM=∠ACE,
在△ABM和△ACE中,
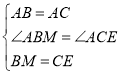 ,
,
∴△ABM≌△ACE(SAS),
∴AM=AE,∠BAM=∠CAE,
∴∠BAM+∠CAM=∠CAE+∠CAM,
即∠MAE=∠BAC=90°,
∵MN=EN,
∴AN⊥EM,AN=![]() EM.
EM.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目