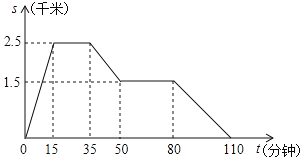
��Ŀ����
����Ŀ��ģ�ͽ�����
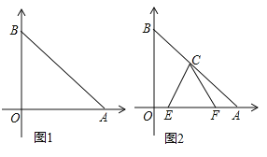
(1)��ͼ1������ֱ��������ABC�У���ACB=90����CB=CA��ֱ��ED������C����A��AD��ED��D����B��BE��ED��E��

��֤����BEC�ա�CDA��
ģ��Ӧ�ã�
(2)��ֱ֪��l1��y=![]() x+4��y�ύ��A�㣬��ֱ��l1����A��˳ʱ����ת45����l2����ͼ2����l2�ĺ�������ʽ��
x+4��y�ύ��A�㣬��ֱ��l1����A��˳ʱ����ת45����l2����ͼ2����l2�ĺ�������ʽ��
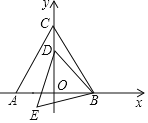
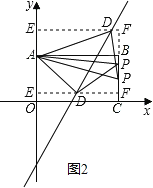
(3)��ͼ3������ABCO��OΪ����ԭ�㣬B������Ϊ(8��6)��A��C�ֱ����������ϣ�P���߶�BC�϶��㣬��PC=m����֪��D�ڵ�һ���ޣ�����ֱ��y=2x-6�ϵ�һ�㣬����APD�Dz���AΪֱ�Ƕ���ĵ���Rt������ֱ��д����D�����꣮
���𰸡�(1)֤����������(2)y=![]() x+4��(3)(4��2)��(
x+4��(3)(4��2)��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��
��������
��1���ȸ�����ABCΪ����ֱ�������εó�CB=CA������AAS������֪��ACD�ա�CBE��
��2������B��BC��AB�ڵ�B����l2�ڵ�C����C��CD��x����D�����ݡ�BAC=45����֪��ABCΪ����Rt�����ɣ�1����֪��CBD�ա�BAO����ȫ�������ε����ʵó�C�����꣬���ô���ϵ�������ֱ��l2�ĺ�������ʽ���ɣ�
��3������DΪֱ�Ƕ��㣬�ֵ�D�ھ���AOCB���ڲ����ⲿ�����������PΪֱ�Ƕ��㣬��Ȼ��ʱ��Dλ�ھ���AOCB���ⲿ���ɴ˿ɵó����ۣ�
(1)�ߡ�ABCΪ����ֱ�������Σ�
��CB=CA��
�֡�AD��CD��BE��EC��
���D=��E=90������ACD+��BCE=180��-90��=90����
�֡ߡ�EBC+��BCE=90����
���ACD=��EBC��
����ACD����CBE��
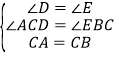 ��
��
���ACD�ա�EBC(AAS)��
(2)����B��BC��AB�ڵ�B����l2�ڵ�C����C��CD��x����D��
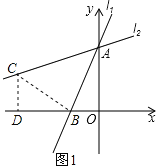 ��ͼ1��
��ͼ1��
�ߡ�BAC=45����
���ABC����Rt����
��(1)��֪����CBD�ա�BAO��
��BD=AO��CD=OB��
��ֱ��l1��y=![]() x+4��
x+4��
��A(0��4)��B(-3��0)��
��BD=AO=4��CD=OB=3��
��OD=4+3=7��
��C(-7��3)��
��l2�Ľ���ʽΪy=kx+b(k��0)��
��![]() ��
��
��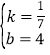 ��
��
��l2�Ľ���ʽ��y=![]() x+4��
x+4��
(3)����Dλ��ֱ��y=2x-6��ʱ�������������
�ٵ�DΪֱ�Ƕ��㣬�����������
����D�ھ���AOCB���ڲ�ʱ����D��x���ƽ����EF����ֱ��OA��E����ֱ��BC��F����D(x��2x-6)��
��OE=2x-6��AE=6-(2x-6)=12-2x��DF=EF-DE=8-x��
����ADE�ա�DPF����DF=AE������
12-2x=8-x��x=4��
��D(4��2)��
����D�ھ���AOCB���ⲿʱ����D(x��2x-6)��
��OE=2x-6��AE=OE-OA=2x-6-6=2x-12��DF=EF-DE=8-x��
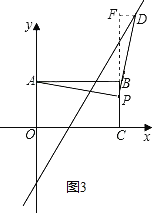
ͬ1��֪����ADE�ա�DPF��
��AE=DF������2x-12=8-x��x=![]() ��
��
��D(![]() ��
��![]() )��
)��
�ڵ�PΪֱ�Ƕ��㣬��Ȼ��ʱ��Dλ�ھ���AOCB���ⲿ��
���D(x��2x-6)����CF=2x-6��BF=2x-6-6=2x-12��
ͬ(1)�ɵã���APB�ա�PDF��
��AB=PF=8��PB=DF=x-8��
��BF=PF-PB=8-(x-8)=16-x��
����������ʾBF��ʽ�ӿɵã�
2x-12=16-x����x=![]() ��
��
��D(![]() ��
��![]() )��
)��
�ۺ�������������ɵã����ڷ��������ĵ���ֱ�������Σ�
��D���������(4��2)��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��

 ��У����ϵ�д�
��У����ϵ�д�