题目内容
【题目】已知点A、B分别在x轴和y轴上,OA=OB,点C为AB的中点,AB=![]()
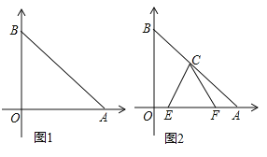
(1) 如图1,求![]() 的面积.
的面积.
(2) 如图2,E、F分别为![]() 上的动点,且∠ECF=45°,求证:
上的动点,且∠ECF=45°,求证:![]()
【答案】(1)72(2)见解析
【解析】
(1)根据等腰直角三角形的性质即可求解;(2)连接OC,在OB上截取OM=AF,连接CM、ME,通过证得△ACF≌△OCM,得出CM=AF,∠OCM=∠ACF,再通过角度的计算得出∠ECM=∠ECF=45°,得到△ECF≌△ECM,得出ME=EF,然后在Rt△MOE中通过勾股定理证明.
(1)∵OA⊥OB
∴OA2+OB2=AB2
∵OA=OB, AB=![]()
∴2OA2 =AB2
∴AO=BA=12
故S△ABO=![]()
(2)连接OC,在OB上截取OM=AF,连接CM、ME,如图2,
∵△AOB, △COA, △OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC,
在△ACF和△OCM中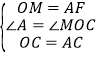
∴△ACF≌△OCM,
∴CM=CF,∠OCM=∠ACF,
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF
在△ECF和△ECM中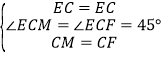
∴△ECF≌△ECM,∴ME=EF,
在Rt△MOE中,∠MOE=90°,
∴![]()

练习册系列答案
相关题目







