题目内容
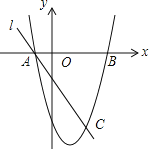
【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900 , 且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。
【答案】
(1)证明:∵△ABC是等腰直角三角形
∴∠ACB=900 , AC=BC
∴∠ACO+∠BCE=900
BE⊥CE,∴∠BCE+∠CBE=900
∴∠ACO=∠CBE
∴△AOC≌△CEB
(2)解:∵△AOC≌△CEB
∴BE=OC=2,CE=OA=4
∴点B的坐标为(6,2)
又一次函数y=x+b经过点B(6,2)
∴2=6+b
∴b=-4
∴点D的坐标为(0,-4)
∴ ![]()
在△ABD中,AD边上高的长度就是B点纵坐标的绝对值.
∴S△ABD= ![]() ×8×6=24
×8×6=24
∴△ABD的面积为24
【解析】(1)由等腰直角三角形的性质可证得AC=BC,∠ACO=∠CBE,进而可证得△AOC≌△CEB;(2)由(1)的全等,可得B坐标,代入解析式,可求出b,进而求出D坐标,AD的长,AD边上高的长度就是B点纵坐标,进而求出面积.

练习册系列答案
相关题目