题目内容
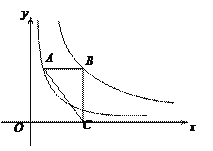
【题目】某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
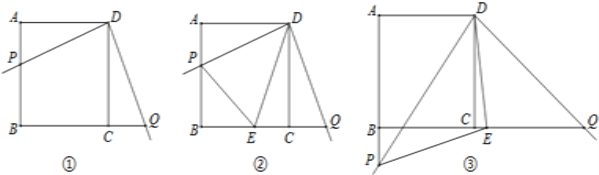
(1)求证:DP=DQ;
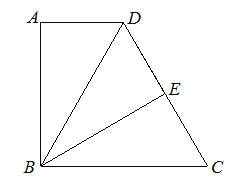
(2)如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
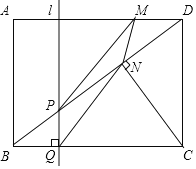
(3)如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
【答案】(1)见解析;(2)PE=QE,理由见解析;(3)![]()
【解析】
(1)证明△ADP≌△CDQ,即可得到结论:DP=DQ.
(2)证明△DEP≌△DEQ,即可得到结论:PE=QE.
(3)与(1)(2)同理,可以分别证明△ADP≌△CDQ、△DEP≌△DEQ.在Rt△BPE中,利用勾股定理求出PE(或QE)的长度,从而可求得![]() ,而△DEP≌△DEQ,所以S△DEP=S△DEQ=
,而△DEP≌△DEQ,所以S△DEP=S△DEQ=![]() .
.
解:(1)证明:
∵∠ADC=∠PDQ=90°,
∴∠ADP=∠CDQ.
在△ADP与△CDQ中,
∵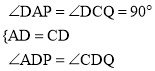 ,
,
∴△ADP≌△CDQ(ASA).
∴DP=DQ.
(2)猜测:PE=QE.
证明如下:
由(1)可知,DP=DQ.
在△DEP与△DEQ中,
∵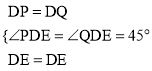 ,
,
∴△DEP≌△DEQ(SAS).
∴PE=QE.
(3)∵AB:AP=3:4,AB=6,
∴AP=8,BP=2.
与(1)同理,可以证明△ADP≌△CDQ,
∴CQ=AP=8.
与(2)同理,可以证明△DEP≌△DEQ
,∴PE=QE.
设QE=PE=x,则![]() .
.
在Rt△BPE中,由勾股定理得:BP2+BE2=PE2,即:![]() ,
,
解得:![]() ,即QE=
,即QE=![]() .
.
∴![]() .
.
∵△DEP≌△DEQ,
∴S△DEP=S△DEQ=![]() .
.

【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.
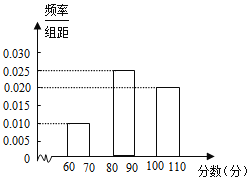
【题目】某社区为了加强居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与作答《2020年新型冠状病毒肺炎的防护全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从该社区抽取40名居民的答卷,并对他们的成绩(单位:分)进行整理、分析,过程如下:
收集数据
85 65 95 100 90 95 85 65 75 85 100 90 70 90 100 80 80 100 95 75 80 100 80 95 65 100 90 95 85 80 100 75 60 90 70 80 95 75 100 90
整理数据(每组数据可含最低值,不含最高值)
分组(分) | 频数 | 频率 |
60~70 | 4 | 0.1 |
70~80 | a | b |
80~90 | 10 | 0.25 |
90~100 | c | d |
100~110 | 8 | 0.2 |
分析数据
(1)填空:a= ,b= ,c= ,d= ;
(2)补全频率分布直方图;
(3)由此估计该社区居民在线答卷成绩在 (分)范围内的人数最多;
(4)如果该社区共有800人参与答卷,那么可估计该社区成绩在90分及以上约为 人.