题目内容
(2013•淄博)矩形纸片ABCD中,AB=5,AD=4.
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).
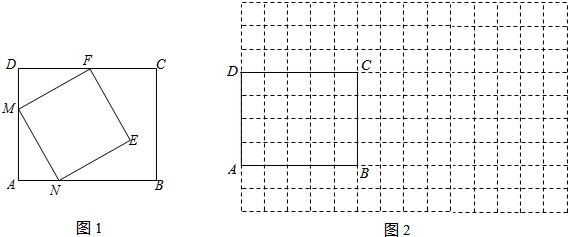
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).

分析:(1)设AM=x(0≤x≤4)则MD=4-x,根据正方形的性质就可以得出Rt△ANM≌Rt△DMF.根据正方形的面积就可以表示出解析式,由二次函数的性质就可以求出其最值;
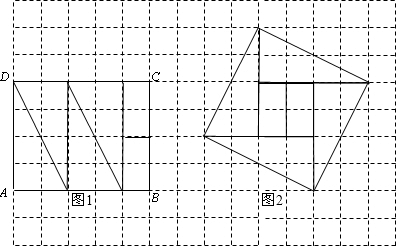
(2)先将矩形纸片分割成4个全等的直角三角形和两个矩形如图,根据赵爽弦图的构图方法就可以拼成正方形.
(2)先将矩形纸片分割成4个全等的直角三角形和两个矩形如图,根据赵爽弦图的构图方法就可以拼成正方形.
解答:解:(1)正方形的最大面积是16.设AM=x(0≤x≤4),则MD=4-x.
∵四边形MNEF是正方形,
∴MN=MF,∠AMN+∠FMD=90°.
∵∠AMN+∠ANM=90°,
∴∠ANM=∠FMD.
∵在△ANM和△DMF中
,
∴△ANM≌△DMF(AAS).
∴DM=AN.
∴S正方形MNEF=MN2=AM2+AN2,
=x2+(4-x)2,
=2(x-2)2+8
∵函数 S正方形MNEF=2(x-2)2+8的开口向上,
对称轴是x=2,
在对称轴的左侧S随x的增大而减小,在对称轴的右侧S随x的增大而增大,
∵0≤x≤4,
∴当x=0或x=4时,
正方形MNEF的面积最大.
最大值是16.
(2)先将矩形纸片ABCD分割成4个全等的直角三角形和两个矩形如图1,然后拼成如图2的正方形.
∵四边形MNEF是正方形,
∴MN=MF,∠AMN+∠FMD=90°.
∵∠AMN+∠ANM=90°,
∴∠ANM=∠FMD.
∵在△ANM和△DMF中
|
∴△ANM≌△DMF(AAS).
∴DM=AN.
∴S正方形MNEF=MN2=AM2+AN2,
=x2+(4-x)2,
=2(x-2)2+8
∵函数 S正方形MNEF=2(x-2)2+8的开口向上,
对称轴是x=2,
在对称轴的左侧S随x的增大而减小,在对称轴的右侧S随x的增大而增大,
∵0≤x≤4,
∴当x=0或x=4时,
正方形MNEF的面积最大.
最大值是16.
(2)先将矩形纸片ABCD分割成4个全等的直角三角形和两个矩形如图1,然后拼成如图2的正方形.

点评:本题考查了全等三角形的判定及性质的运用,勾股定理的运用,二次函数的解析式的运用,拼图的运用,在解答本题时由正方形的性质建立二次函数是求最值的关键.

练习册系列答案
相关题目


 (2013•淄博)如图,矩形AOBC的面积为4,反比例函数
(2013•淄博)如图,矩形AOBC的面积为4,反比例函数