题目内容
如图,P是⊙O的直径AB延长线上的一点, PC切⊙O于点C,弦CD⊥AB,垂足为点E,若 ,
,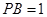 .
.


求:(1)⊙O的半径;
(2)CD的长;
(3)图中阴影部分的面积.
 ,
,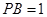 .
.

求:(1)⊙O的半径;
(2)CD的长;
(3)图中阴影部分的面积.
(1)1;(2) ;(3)
;(3)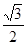 -
-
 ;(3)
;(3)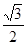 -
-
试题分析:(1)连接OC,根据切线的性质可得OC⊥PC,设OC=OB=r,根据勾股定理即可列方程求解;
(2)先证得△COE∽△POC,根据相似三角形的性质即可求得CE的长,再根据垂径定理即可求得结果;
(3)先根据OC、OP的长度的关系得到∠COP的度数,即可求得扇形OCB的面积,用直角△POC的面积减去扇形OCB的面积即可求得结果.
(1)连接OC

∵PC切⊙O于点C
∴OC⊥PC
设OC=OB=r,由题意得

解得
 ;
;(2)∵OC⊥PC,CD⊥AB,∠COP=∠COE
∴△COE∽△POC
∴
 ,即
,即
解得

∵CD⊥AB
∴

(3)∵OC=1,OP=2,

∴∠COP=60°
∴图中阴影部分的面积
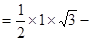

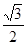 -
-
点评:解答本题的关键是熟练掌握切线垂直于经过切点的半径;相似三角形的对应边成比例,注意对应字母在对应位置上.

练习册系列答案
相关题目
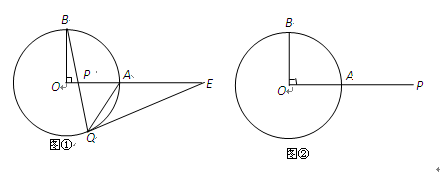
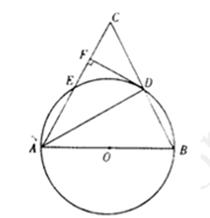
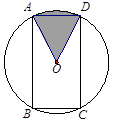
 ,BC=1,求图中阴影部分所表示的扇形OAD的面积.
,BC=1,求图中阴影部分所表示的扇形OAD的面积.