题目内容
已知两条直线 和
和 .
.
⑴在同一坐标系内作出它们的图象;
⑵求出它们的交点 坐标;
坐标;
⑶求出这两条直线与 轴围成的三角形的面积;
轴围成的三角形的面积;

 和
和 .
.⑴在同一坐标系内作出它们的图象;
⑵求出它们的交点
 坐标;
坐标;⑶求出这两条直线与
 轴围成的三角形的面积;
轴围成的三角形的面积;
⑴列表略,图象
⑵
解得
∴ (3,2)
(3,2)
⑶
答:这两条直线与 轴围成的三角形的面积为8个平方单位
轴围成的三角形的面积为8个平方单位

⑵

解得

∴
 (3,2)
(3,2)⑶

答:这两条直线与
 轴围成的三角形的面积为8个平方单位
轴围成的三角形的面积为8个平方单位
(1)利用列表、描点、连线即可作出函数的图象;
(2)将两函数组成一个方程组后求得方程组的解即可求得交点的坐标;
(3)求得函数与x轴的交点坐标即可求得线段BC的长,A点的纵坐标即为三角形的高,据此可以求得三角形的面积.
(2)将两函数组成一个方程组后求得方程组的解即可求得交点的坐标;
(3)求得函数与x轴的交点坐标即可求得线段BC的长,A点的纵坐标即为三角形的高,据此可以求得三角形的面积.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 取什么值,直线
取什么值,直线 :y=
:y= 时,靠近原点O一侧的那部分面积.
时,靠近原点O一侧的那部分面积.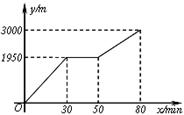
 (元)与销售量
(元)与销售量 (支)之间的函数关系式;
(支)之间的函数关系式; (元)与销售量
(元)与销售量 的图像过点(1,-2),则关于
的图像过点(1,-2),则关于 的不等式
的不等式 的解集是 .
的解集是 . 中,如果
中,如果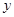 随
随 增大而减小,那么常数
增大而减小,那么常数 的取值范围是( )
的取值范围是( ) .
. ;
;  .
. ;
;  .
. ;
;  .
. .
. (亩)与补贴数额
(亩)与补贴数额 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额 (元)会相应降低,且
(元)会相应降低,且
 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额