题目内容
【题目】如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB，BC，CA至点A1 ， B1 ， C1 ， 使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1 ， B1 ， C1 ， 得到△A1B1C1 ， 记其面积为S1；第二次操作，分别延长A1B1 ， B1C1 ， C1A1至点A2 ， B2 ， C2 ， 使得A2B1=2A1B1 ， B2C1=2B1C1 ， C2A1=2C1A1 ， 顺次连接A2 ， B2 ， C2 ， 得到△A2B2C2 ， 记其面积为S2 ， 则S2＝。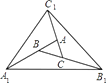
【答案】361
【解析】解 : 
连接A1C，根据同高三角形面积的比等于底的比，得出△ABC的面积∶△A1CB的面积=AB∶A1B=1:2,又△ABC的面积等于1，故△A1CB的面积为2，同理△A1B1C的面积为4，故△A1B1B的面积等于6，同理△CB1C1的面积,△A1C1A的面积都是6，从而得出 S 1 = 19 S Δ A B C , 同理 S 2 = 19 S 1 = 361。
练习册系列答案
相关题目
【题目】我市某工艺厂为配合北京奥运，设计了一款成本为20元∕件的工艺品投放市场进行试销．经过调查，得到如下数据：
销售单价x（元/件） | … | 30 | 40 | 50 | 60 | … |
每天销售量y（件） | … | 500 | 400 | 300 | 200 | … |
（1）把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；
（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？（利润=销售总价﹣成本总价）
（3）当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？
