题目内容
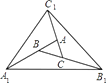
【题目】如图,在△ABC中,AB=BC , BD平分∠ABC . 过点D作AB的平行线,过点B作AC的平行线,两平行线相交于点E , BC交DE于点F , 连接CE . 求证:四边形BECD是矩形.
【答案】证明:∵AB=BC,BD平分∠ABC
∴AD=DC,BD⊥CA
∵AB∥DE, AD∥BE
∴四边形ABED是平行四边形
∴AD=BE,AD∥BE, AB=DE
∴DC=BE,DC∥BE
∴四边形BECD是平行四边形
∵BD⊥CA
∴∠BDC=90°![]()
∴四边形BECD是矩形
【解析】根据已知条件易推知四边形BECD是平行四边形. 结合等腰△ABC“三线合一”的性质证得BD⊥AC,即∠BDC=90°,由“有一内角为直角的平行四边形是矩形”得到◇BECD是矩形.
【考点精析】本题主要考查了角平分线的性质定理和等腰三角形的性质的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目