题目内容
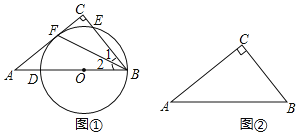
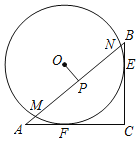
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3．直径为5的⊙O分别与AC、BC相切于点F、E，与AB交于点M、N，过点O作OP⊥MN于P，则OP的长为（ ）
A.1B.
C.
D.
【答案】B
【解析】
连结OE，OF，则四边形OFCE为正方形，可证明△AFG∽△ACB，可求出OG长，证明△OGP∽△ABC可求出OP的长．
解：连结OE，OF，
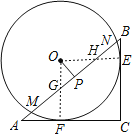
∵⊙O分别与AC、BC相切于点F、E，
∴OE⊥BC，OF⊥AC，
∵OE＝OF，
∴四边形OFCE为正方形，
∵⊙O的直径为5
∴
设FG＝x，
∵FG∥BC，
∴△AFG∽△ACB，
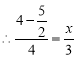
解得x＝
，
∴OG＝
，
∵∠OGP＝∠AGF＝∠ABC，
∴△OGP∽△ABC，
∴
，
在Rt△ABC中，
∵∠ACB＝90°，AC＝4，BC＝3
∴
，
∴
．
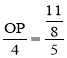故选：B．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
