题目内容
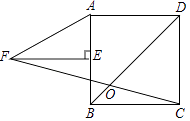
【题目】如图,正方形ABCD中,F为BC边上的中点,连接AF交对角线BD于G,在BD上截BE=BA,连接AE,将△ADE沿AD翻折得△ADE′,连接E′C交BD于H,若BG=2,则四边形AGHE′的面积是 . 
【答案】![]() ﹣
﹣ ![]()
【解析】解:如图所示,连接EE',过G作BC的垂线,交BC于M,交AD于N,则MN⊥AD, 由BF∥AD可得,△BGF∽△DGA,
∴ ![]() =
= ![]()
∵BG=2,F是BC的中点,
∴DG=4,BD=6,
∴等腰Rt△ABD中,AB=3 ![]() ,
,
∴BE=BA=3 ![]() ,
,
∴DE=6﹣3 ![]() ,
,
由折叠可得,AD⊥EE',∠EDE'=90°,
∴等腰Rt△DEE'中,EE'= ![]() DE=6
DE=6 ![]() ﹣6,
﹣6,
△DEE'的面积= ![]() DE2=
DE2= ![]() (6﹣3
(6﹣3 ![]() )2=27﹣18
)2=27﹣18 ![]() ,
,
由EE'∥CD,可得△EE'H∽△DCE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =2﹣
=2﹣ ![]() ,
,
∴△DE'H的面积=△DEE'的面积× ![]() =(27﹣18
=(27﹣18 ![]() )×
)× ![]() =
= ![]() ,
,
∵Rt△BGM中,GM= ![]() ,
,
∴GN=3 ![]() ﹣
﹣ ![]() =2
=2 ![]() ,
,
∴△ADG的面积= ![]() AD×GN=
AD×GN= ![]() ×3
×3 ![]() ×2
×2 ![]() =6,
=6,
又∵△ADE'的面积= ![]() AD×
AD× ![]() =
= ![]() ×3
×3 ![]() ×(3
×(3 ![]() ﹣3)=9﹣
﹣3)=9﹣ ![]() ,
,
∴四边形AGHE′的面积=△ADG的面积+△ADE'的面积﹣△DE'H的面积=6+(9﹣ ![]() )﹣
)﹣ ![]() =
= ![]() ﹣
﹣ ![]() .
.
所以答案是: ![]() ﹣
﹣ ![]() .
.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 阅读快车系列答案
阅读快车系列答案