��Ŀ����
����Ŀ����ͼ����֪һ��ֱ�߹��㣨0��4��������������y= ![]() x2����A��B���㣬���е�A�ĺ������ǩ�2��
x2����A��B���㣬���е�A�ĺ������ǩ�2��
��1��������ֱ�ߵĺ�����ϵʽ����B�����꣮
��2����x�����Ƿ���ڵ�C��ʹ�á�ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
��3�����߶�AB��һ��P����PM��x�ᣬ���������ڵ�M����M�ڵ�һ���ޣ���N��0��1��������M�ĺ�����Ϊ��ֵʱ��MN+3MP�ij���������ֵ�Ƕ��٣�
���𰸡�
��1��
�⣺�ߵ�A��ֱ���������ߵĽ��㣬�Һ�����Ϊ��2��
��y= ![]()
![]() ����2��2=1��A�����������2��1����
����2��2=1��A�����������2��1����
��ֱ�ߵĺ�����ϵʽΪy=kx+b��
����0��4��������2��1������� ![]() ��
��
��� ![]() ��
��
��ֱ��y= ![]() x+4��
x+4��
��ֱ�����������ཻ��
�� ![]() x+4=
x+4= ![]() x2��
x2��
��ã�x=��2��x=8��
��x=8ʱ��y=16��
���B��������8��16��
��2��
�⣺��ͼ1������B��BG��x�ᣬ����A��AG��y�ᣬ����ΪG��
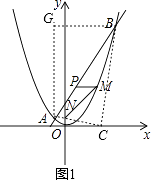
��AG2+BG2=AB2��
����A����2��1����B��8��16�������AB2=325��
���C��m��0����ͬ���ɵ�AC2=��m+2��2+12=m2+4m+5��
BC2=��m��8��2+162=m2��16m+320��
������BAC=90�㣬��AB2+AC2=BC2����325+m2+4m+5=m2��16m+320��
��ã�m=�� ![]() ��
��
������ACB=90�㣬��AB2=AC2+BC2����325=m2+4m+5+m2��16m+320��
��ã�m=0��m=6��
������ABC=90�㣬��AB2+BC2=AC2����m2+4m+5=m2��16m+320+325��
��ã�m=32��
���C���������� ![]() ��0������0��0������6��0������32��0��
��0������0��0������6��0������32��0��
��3��
�⣺��M��a�� ![]() a2������ͼ2��
a2������ͼ2��
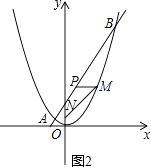
��MP��y�ύ�ڵ�Q��
��Rt��MQN�У��ɹ��ɶ�����MN= ![]() =
= ![]() a2+1��
a2+1��
�֡ߵ�P���M��������ͬ��
�� ![]() +4=
+4= ![]() a2��
a2��
��x= ![]() ��
��
���P�ĺ�����Ϊ ![]() ��
��
��MP=a�� ![]() ��
��
��MN+3PM= ![]() +1+3��a��
+1+3��a�� ![]() ��=��
��=�� ![]() a2+3a+9��
a2+3a+9��
�൱a=�� ![]() =6��
=6��
�֡ߩ�2��6��8��
��ȡ�����ֵ18��
�൱M�ĺ�����Ϊ6ʱ��MN+3PM�ij��ȵ����ֵ��18
����������1��������õ�A�����꣬Ȼ�����ô���ϵ����ȷ��ֱ�ߵĽ���ʽ���Ӷ����ֱ���������ߵĽ������ꣻ��2����ͼ1������B��BG��x�ᣬ����A��AG��y�ᣬ����ΪG��Ȼ�������BAC=90�㣬��AB2+AC2=BC2������ACB=90�㣬��AB2=AC2+BC2������ABC=90�㣬��AB2+BC2=AC2����������m��ֵ���Ӷ�ȷ����C�����ꣻ��3����M��a�� ![]() a2������ͼ2����MP��y�ύ�ڵ�Q��������Rt��MQN�У��ɹ��ɶ�����MN=
a2������ͼ2����MP��y�ύ�ڵ�Q��������Rt��MQN�У��ɹ��ɶ�����MN= ![]() a2+1��Ȼ����ݵ�P���M��������ͬ�õ�x=
a2+1��Ȼ����ݵ�P���M��������ͬ�õ�x= ![]() ���Ӷ��õ�MN+3PM=��
���Ӷ��õ�MN+3PM=�� ![]() a2+3a+9��ȷ�����κ�������ֵ���ɣ�
a2+3a+9��ȷ�����κ�������ֵ���ɣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�