��Ŀ����
����Ŀ��������̽����
��1���������ϵĵ�P�������²������Ȱѵ�P��ʾ��������![]() ���ٰ���������Ӧ�ĵ�����ƽ��1����λ���õ���P�Ķ�Ӧ��P�䣮
���ٰ���������Ӧ�ĵ�����ƽ��1����λ���õ���P�Ķ�Ӧ��P�䣮
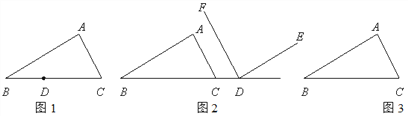
��A��B�������ϣ����߶�AB�ϵ�ÿ�����������������õ��߶�A��B�䣬���е�A��B�Ķ�Ӧ��ֱ�ΪA�䣬B�䣮��ͼ1������A��ʾ�����ǩ�3�����A���ʾ�������� ��������B���ʾ������2�����B��ʾ�������� ������֪�߶�AB�ϵĵ�E��������������õ��Ķ�Ӧ��E�����E�غϣ����E��ʾ�������� ����

��2����ͼ2����ƽ��ֱ������ϵxOy�У���������ABCD�����ڲ���ÿ����������²�������ÿ����ĺᡢ�����궼����ͬһ��ʵ��a�����õ��ĵ�������ƽ��m����λ��������ƽ��n����λ��m��0��n��0�����õ�������A��B��C��D�估���ڲ��ĵ㣬���е�A��B�Ķ�Ӧ��ֱ�ΪA�䣬B�䣮��֪������ABCD�ڲ���һ����F��������������õ��Ķ�Ӧ��F�����F�غϣ����F�����꣮
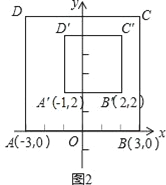
���𰸡���1��0��3�� ![]() ����2��F�������Ϊ(1��4)��
����2��F�������Ϊ(1��4)��
�������������������1��������Ŀ�涨���Լ������ϵ�������ƽ�Ƶļ�����������A�䣻���ݵ�B����ʾ���������ù涨���㼴�ɵã����E��ʾ����Ϊb�����������г����̼��㼴�ɵý⣻
��2���ȸ�������ƽ�ƺ����겻�䣬������ӣ�����ƽ�ƺ�����ӣ������겻�����ƽ�ƹ��ɣ�Ȼ�����F������Ϊ��x��y��������ƽ�ƹ����г���������⼴�ɣ�
�����������1��A�䣺-3��![]() +1=0;B����2-1����
+1=0;B����2-1����![]() =3��E�����E��ʾ����Ϊb�����У�b=
=3��E�����E��ʾ����Ϊb�����У�b= ![]() +1�����b=
+1�����b=![]() ��
��
��2����������n=2����3a+m=��1��3a��m=2����a=![]() ��m=
��m=![]() ��n=2��
��n=2��
��F(x��y)���������⣬��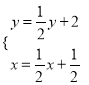 �����
�����![]() ��
��
��F�������Ϊ(1��4)��

����Ŀ������һ����ͯ�ڣ�ij��߳���������һ����ͼ��ʾ�Ŀ�������ת����ת�̣���չ�н��������˿�����߾��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ��Ʒ���±��Ǹû��һ��ͳ�����ݣ�����˵������ȷ���ǣ�������

ת��ת�̵Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
������Ǧ��������Ĵ���m | 68 | 108 | 140 | 355 | 560 | 690 |
������Ǧ���������Ƶ�� | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
A. ��n�ܴ�ʱ������ָ��������Ǧ���������Ƶ�ʴ�Լ��0.70
B. ������ȥת��ת��һ�Σ����Ǧ�ʵĸ��ʴ�Լ��0.70
C. ���ת��ת��2000�Σ�ָ���������ľߺ�������Ĵ�����Լ��600��
D. ת��ת��10�Σ�һ����3�λ���ľߺ�
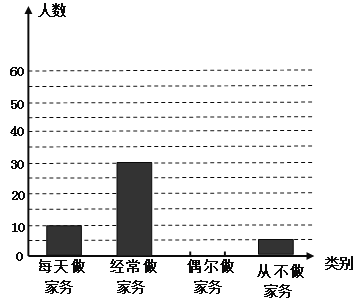
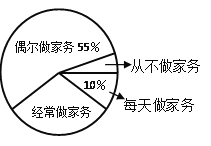
����Ŀ��ijѧУ����־Ը��Э��Ը��г����Ŀ����������е��飬��ȫ��365���������ȡ��80��Ŀ�������ָ����AQI�����ݣ����Ƴ�������������ͳ��ͼ���������ͼ�����ṩ����Ϣ����������⣺
AQIָ�� | �����ȼ� | �������죩 |
0��50 | �� | m |
51��100 | �� | 44 |
101��150 | �����Ⱦ | n |
151��200 | �ж���Ⱦ | 4 |
201��300 | �ض���Ⱦ | 2 |
300���� | ������Ⱦ | 2 |
��1 ��ͳ�Ʊ���m= ��n= ������ͳ��ͼ�У����������ȼ�Ϊ������������ռ %��
��2����ȫ����ͳ��ͼ����ͨ��������Ƹ��г���ȫ����������ȼ�Ϊ���������������������������죿
��3���ݵ��飬������Ⱦ��2�췢���ڴ����ڼ䣬ȼ���̻������Ϊ������Ⱦ��һ����Ҫԭ�ݴˣ��������һ�����������飮