��Ŀ����
����Ŀ����֪����ABC��ͬһƽ���ڵĵ�D��
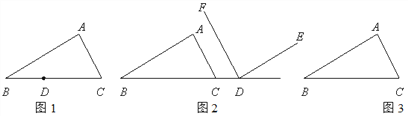
��1����ͼ1����D��BC���ϣ���D��DE��BA��AC��E��DF��CA��AB��F��
�� �����⣬��ͼ1�в�ȫͼ�Σ�
�� �жϡ�EDF���A��������ϵ����ֱ��д�����ۣ�����֤������
��2����ͼ2����D��BC���ӳ����ϣ�DF��CA����EDF=��A���ж�DE��BA��λ�ù�ϵ����֤����
��3����ͼ3����D�ǡ�ABC�ⲿ��һ�����㣬��D��DE��BA��ֱ��AC��E��DF��CA��ֱ��AB��F��ֱ��д����EDF���A��������ϵ������֤������
���𰸡���1���� ��ȫͼ�μ��������� ��EDF=��A��
��2��DE��BA��֤����������
��3����EDF=��A����EDF+��A=180��
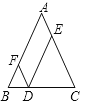
�������������������1���������ⲹȫͼ�μ��ɣ�����ƽ���ı��ε��ж��ɵ��ı���AEDF��ƽ���ı��Σ�����ƽ���ı��ζԽ���ȵý������2���ӳ�BA����ƽ���ߵ����ʵá�2=��3�����������á�1=��3�����ڴ��������ֱ��ƽ�е�DE��BA����3����������ۼ���.
�����������1���� ��ȫͼ�����£�
 ��
��
�� ��EDF=��A.
��DE��BA��DF��CA
���ı���AEDF��ƽ���ı���
���EDF=��A
��2��DE��BA.
֤������ͼ���ӳ�BA��DF��G.
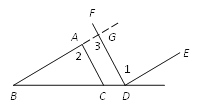
�� DF��CA��
�� ��2=��3.
�֡� ��1=��2��
�� ��1=��3.
�� DE��BA
��3���ɣ�2��֪��EDF=��A��
������D����λ��ʱ��
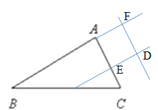
���ı���AEDF��ƽ���ı��Σ�
���BAC=��AFD, ��AFD+��EDF=180��,
���EDF+��BAC=180��