Question

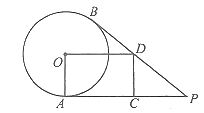
【题目】已知：如图，点是外一点，过点分别作的切线、，切点为点、，连接，过点作交于点，过点作于.

（1）求证：四边形是矩形；

（2）若， 的半径为，试证明四边形的周长等于.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：

（1）由PA是的切线可得∠OAP=90°，结合OD∥AP可得∠O=90°，再结合DC⊥AP即可得到四边形OACD矩形了；

（2）如图，连接OB，由四边形AOCD是矩形结合的半径为可得DC=OA=OB= ，由OD∥AP可得∠BDO=∠P=45°，由PB是的切线可得∠OBD=90°，由此可得BD=OB=r，则OD= =AC，这样即可由OA+AC+DC+OD求得四边形OACD的周长为.

试题解析：

（1）∵是的切线，切点为，

∴，

∵，

∴，

又∵，

∴四边形是矩形；

（2）如图，连接OB，

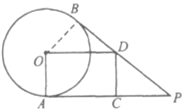
由（1）得，四边形是矩形，

∴，

∵，

∴，

∵是的切线，

∴，

∴，

∴,

在中，由勾股定理得： ，

∴四边形的周长.