Question

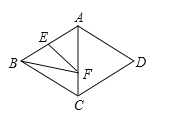
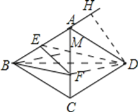
【题目】如图，菱形ABCD的边长为6，∠BAD=120°，点E是AB的中点，点F是AC上的一动点，则EF+BF的最小值是__________．

Answer 1

【答案】

【解析】

首先连接DB，DE，设DE交AC于M，连接MB，DF．证明只有点F运动到点M时，EF+BF取最小值，再根据菱形的性质、勾股定理求得最小值．

连接DB，DE，设DE交AC于M，连接MB，DF，延长BA，DH⊥BA于H，

∵四边形ABCD是菱形，

∴AC，BD互相垂直平分，

∴点B关于AC的对称点为D，

∴FD=FB，

∴FE+FB=FE+FD≥DE．

只有当点F运动到点M时，取等号（两点之间线段最短），

△ABD中，AD=AB，∠DAB=120°，

∴∠HAD=60°，

∵DH⊥AB，

∴AH=AD，DH=AD，

∵菱形ABCD的边长为6，E为AB的中点，

∴AE=3，AH=3，

∴EH=6，DH=，

在Rt△EHD中，DE=，

∴EF+BF的最小值为．

故答案为：．