题目内容
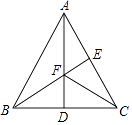
【题目】如图，等边△ABC中，AB=4，E是线段AC上的任意一点，∠BAC的平分线交BC于D，AD=2 
，F是AD上的动点，连接CF、EF，则CF+EF的最小值为 ． 
【答案】2 
【解析】解：∵AD是等边△ABC的∠BAC的平分线，∴AD⊥BC，BD=CD，
∴点B、C关于AD对称，
过点B作BE⊥AC于E，交AD于F，连接CF，
由轴对称确定最短路线问题，点E、F即为使CF+EF的最小值的点，
∵△ABC是等边三角形，AD、BE都是高，
∴BE=AD=2 ，
∴CF+EF的最小值=BE=2 ．
所以答案是：2 ．
【考点精析】通过灵活运用等边三角形的性质和轴对称-最短路线问题，掌握等边三角形的三个角都相等并且每个角都是60°；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径即可以解答此题．
练习册系列答案
相关题目
