题目内容
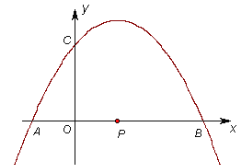
【题目】 (10分)已知抛物线![]() 与
与![]() 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
(1)直接写出抛物线的对称轴,及抛物线与![]() 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式;
(3)坐标平面内是否存在点![]() ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】见解析
【解析】
(1)根据对称轴公式,对称轴x=﹣![]() =1;
=1;
点B的坐标是(3,0).(2分)
(2)点C在以AB为直径的⊙P上,∴∠ACB=90°
由∠ACB=∠AOC=∠COB=90°得△AOC∽△COB,
∴![]() ,
,
∴CO=![]() ,
,
∴b=![]()
当x=﹣1,y=0时,﹣a﹣2a+![]() =0,
=0,
∴a=![]() ,
,
∴y=﹣![]() ;(6分)
;(6分)
(3)点M的坐标有三种情况,如果以AB为平行四边形的对角线,那么P(1,0)就是平行四边开的对称中心,即C点与M点关于P点位对称,设M点坐标为(x,y).
那么![]() ,x=2 .
,x=2 . ![]() ,y=
,y=![]() .∴M点坐标为(2,
.∴M点坐标为(2,![]() )
)
同理以AC、BC为对称轴得出M点的坐标为(-4,![]() )、(4,
)、(4,![]() )
)
分别是:(2,![]() ),(-4,
),(-4,![]() )或(4,
)或(4,![]() ).(10分)
).(10分)


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值.
(2)若用扇形统计图来描述,求分数在8≤m<9内所对应的扇形的圆心角的度数.
(3)将在第一组内的两名选手记为A1,A2,在第四组内的两名选手记为B1,B2, 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率.