题目内容
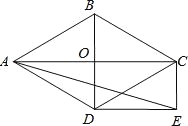
【题目】如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由.

【答案】(1)抛物线解析式为y=-![]() x2+
x2+![]() x,(2)
x,(2)![]() 或
或![]() 或m=
或m=![]() .
.
【解析】
试题分析:(1)先确定出点C,D的坐标,再用待定系数法求出抛物线解析式,
(2)根据题意设出点M的坐标,表示出点N坐标,以A、C、M、N为顶点的四边形为平行四边形只要AC=MN,用它建立方程求出m即可.
试题解析:(1)∵过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点,
∴点C(1,3),D(3,1),
∵抛物线y=ax2+bx+c经过O、C、D三点,
∴c=0,a+b=3,9a+3b=1.
∴a=-![]() ,b=
,b=![]() ,c=0,
,c=0,
∴抛物线解析式为y=-![]() x2+
x2+![]() x,
x,
(2)∵A(1,0),C(3.0),
∴AC=3,
∵AC⊥x轴,MN⊥x轴,
∴AC∥MN,
∵以A、C、M、N为顶点的四边形为平行四边形,
∴AC=MN,
∵点D坐标为(3,1),
∴直线OD解析式为y=![]() x,
x,
∵点M为直线OD上的一个动点,
∴设M(m,![]() m),
m),
∴N(m,-![]() m2+
m2+![]() m),
m),
∴MN=|-![]() m2+
m2+![]() m-
m-![]() m|=
m|=![]() |4m2-12m|,
|4m2-12m|,
∵AC=MN,
∴![]() |4m2-12m|=3,
|4m2-12m|=3,
∴|4m2-12m|=9,
①当4m2-12m>0时,即m<0,或m>4,
∴4m2-12m=9,
∴m=![]() ,
,
∴点M的横坐标为![]() 或
或![]() ,
,
②当4m2-12m<0时,即0<m<4,
∴4m2-12m=-9,
∴m=![]() ,
,
即:存在符合条件的点M,求此时点M的横坐标为![]() 或
或![]() 或m=
或m=![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案