题目内容
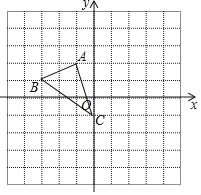
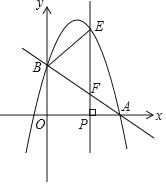
【题目】如图，在平面直角坐标系中，直线y＝-
x+2分别交x轴、y轴于点A、B，抛物线y＝﹣x2+bx+c经过点A、B．点P是x轴上一个动点，过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F．设点P的横坐标为m．
（1）点A的坐标为 ．
（2）求这条抛物线所对应的函数表达式．
（3）点P在线段OA上时，若以B、E、F为顶点的三角形与△FPA相似，求m的值．
（4）若E、F、P三个点中恰有一点是其它两点所连线段的中点（三点重合除外），称E、F、P三点为“共谐点”．直接写出E、F、P三点成为“共谐点”时m的值．
【答案】（1）（4，0）（2）y＝﹣x2+
x+2（3）
，（4）﹣1或﹣
或
【解析】
（1）令y＝0，即可求出交点坐标,
（2）将A（4，0），B（0，2）代入y＝﹣x2+bx+c中,即可求出函数解析式,（3）根据
分类讨论,
得
得
,即可求解,（4）根据当F为线段PE的中点时，当P为线段FE的中点时，当E为线段FP的中点时分类讨论解题即可.
（1）在y＝-x+2中，令y＝0，则x＝4，
∴A（4，0）；
故答案为：（4，0）；
（2）∵在y＝-x+2中，令x＝0，则y＝2，
∴B（0，2），
把A（4，0），B（0，2）代入y＝﹣x2+bx+c，得b＝，
∴这条抛物线所对应的函数表达式为y＝﹣x2+x+2；
（3）∵P（m，0），E（m，﹣m2+m+2），F（m，﹣m+2），
∵且∠BFE＝∠AEP，
∴∠BEP＝∠APF＝90°或∠EBF＝∠APF＝90°，
则有BE⊥PE，
∴E点的纵坐标为2，
∴
解得m＝0（舍去）或m＝，
如图1，
过点E作EC⊥y轴于点C，
则∠EBC+∠BEC＝90°，EC＝m，BC＝﹣m2+m+2﹣2＝﹣m2+m，
∵∠EBF＝90°，
∴∠EBC+∠ABO＝90°，
∴∠ABO＝∠BEC，
∴Rt△ECB∽Rt△BOA，
∴
,
∴
,解得m＝0（舍去）或m＝，
解得，m＝，
综上所述，以B、E、F为顶点的三角形与△FPA相似，m的值＝，
（4）由（1）知，P（m，0），E（m，﹣m2+m+2），F（m，﹣m+2），
∵E、F、P三点为“共谐点”，
∴有F为线段PE的中点、P为线段FE的中点或E为线段PF的中点，
当F为线段PE的中点时，则有2（﹣m+2）＝﹣m2+m+2，解得m＝4（三点重合，舍去）或m＝；
当P为线段FE的中点时，则有﹣m+2+（﹣m2+m+2）＝0，解得m＝4（舍去）或m＝﹣1；
当E为线段FP的中点时，则有﹣m+2＝2（﹣m2+m+2），解得m＝4（舍去）或m＝﹣；
综上可知当E、F、P三点成为“共谐点”时m的值为﹣1或﹣或．
