题目内容
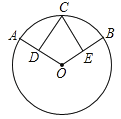
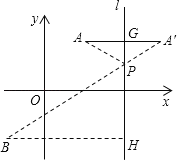
【题目】(定义)如图1,A,B为直线l同侧的两点,过点A作直线l的对称点![]() ,连接
,连接![]() B交直线l于点P,连接AP,则称点P为点A,B关于直线
B交直线l于点P,连接AP,则称点P为点A,B关于直线![]() 的“等角点”.
的“等角点”.
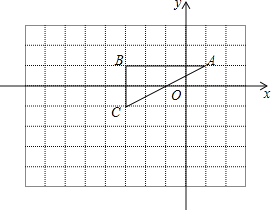
(运用)如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(-2,-
),B(-2,-![]() )两点.
)两点.
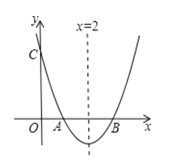
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() )三点中,点 是点A,B关于直线x=4的等角点;
)三点中,点 是点A,B关于直线x=4的等角点;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的等角点,其中m>2,∠APB=α,求证:![]() ;
;
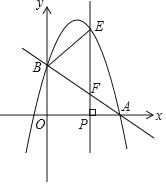
(3)若点P是点A,B关于直线y=ax+b(a≠0)的等角点,且点P位于直线AB的右下方,当∠APB=60°时,求b的取值范围(直接写出结果).

【答案】(1)C;(2)证明见解析;(3)见解析.
【解析】
(1)根据“等角点”的定义找到A关于x=4的对称点A',连接A'B,求得与x=4的交点即可;
(2)根据“等角点”的定义和三角函数的知识,再利用△APG∽△BPH,即可得到;
(3)构造辅助圆⊙O解题,当直线y=ax+b与⊙O相交的另一个交点为Q时,利用圆周角定理以及对称性可证明△ABQ为等边三角形,从而确定Q为定点.再过A,Q分别作y轴的垂线,构造相似三角形(Rt△AMO∽Rt△ONQ),利用相似三角形对应边成比例即可求出Q的坐标,再利用待定系数法求出BQ和AQ的解析式,由此即可确定b的取值范围.
解:(1)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]()
![]() 直线
直线![]() 解析式为:
解析式为:![]()
当![]() 时,
时,![]()
故答案为:![]()
(2)如图,过点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,连
,连![]() ,交直线
,交直线![]() 于点
于点![]()
作![]() 于点
于点![]()
![]() 点
点![]() 和
和![]() 关于直线
关于直线![]() 对称
对称
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ,
,![]()
![]()
在![]() 中,
中,![]()
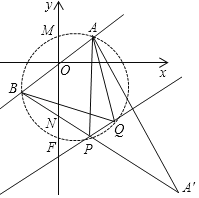
(3)如图,当点![]() 位于直线
位于直线![]() 的右下方,
的右下方,![]() 时,
时,
点![]() 在以
在以![]() 为弦,所对圆周为
为弦,所对圆周为![]() ,且圆心在
,且圆心在![]() 下方
下方
若直线![]() 与圆相交,设圆与直线
与圆相交,设圆与直线![]() 的另一个交点为
的另一个交点为![]()
由对称性可知:![]() ,
,
又![]()
![]()
![]() ,
,![]()
![]()
![]() 是等边三角形
是等边三角形
![]() 线段
线段![]() 为定线段
为定线段
![]() 点
点![]() 为定点
为定点
若直线![]() 与圆相切,易得
与圆相切,易得![]() 、
、![]() 重合
重合
![]() 直线
直线![]() 过定点
过定点![]()
连![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 、
、![]()
![]() ,
,![]()
![]()
![]() 是等边三角形
是等边三角形
![]() ,
,![]()
![]()
又![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() 点坐标为
点坐标为![]()
设直线![]() 解析式为
解析式为![]()
将![]() 、
、![]() 坐标代入得
坐标代入得
![]()
解得
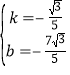
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() .
.
设直线![]() 的解析式为:
的解析式为:![]() ,
,
将![]() 、
、![]() 两点代入
两点代入![]() ,
,
解得![]() .
.
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() .
.
若点![]() 与
与![]() 点重合,则直线
点重合,则直线![]() 与直线
与直线![]() 重合,此时,
重合,此时,![]() .
.
若点![]() 与点
与点![]() 重合,则直线
重合,则直线![]() 与直线
与直线![]() 重合,此时,
重合,此时,![]() .
.
又![]() ,且点
,且点![]() 位于
位于![]() 右下方,
右下方,
![]() 且
且![]() 或
或![]() .
.