题目内容
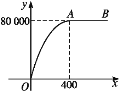
【题目】某厂家生产一种产品,月初需要一次性投资25 000元,每生产一件产品需增加投入100元.设x(件)是月生产量,y(元)是销售完x件产品所得的总销售额,y与x的关系如图中的图象所示,图象中从点O到点A的部分是抛物线的一部分,且点A是抛物线的顶点,点A后面的部分与x轴平行.
(1)求y关于x的函数关系式;
(2)设月纯利润为z,求z关于x的函数关系式;
(3)当月产量为多少件时,厂家所获利润最大?最大利润为多少元?
【答案】(1)y=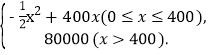 (2)z=
(2)z= ;(3) 当月产量为300台时,利润最大,最大利润为20 000元
;(3) 当月产量为300台时,利润最大,最大利润为20 000元
【解析】
(1)根据顶点坐标设二次函数的解析式为y=a(x-400)2+80000,把O(0,0)代入可求出a的值,即可得![]() 时y关于x的函数关系式,由点A后面的部分与x轴平行可得x>400时y关于x的函数关系式;(2)根据月纯利润=总销售额-月初投资-产品成本即可得出答案;(3)分别计算x>400时和
时y关于x的函数关系式,由点A后面的部分与x轴平行可得x>400时y关于x的函数关系式;(2)根据月纯利润=总销售额-月初投资-产品成本即可得出答案;(3)分别计算x>400时和![]() 时利润的最大值即可.
时利润的最大值即可.
(1)当![]() 时,设函数解析式为y=a(x-400)2+80000,
时,设函数解析式为y=a(x-400)2+80000,
∵图像经过O(0,0),
∴a(x-400)2+80000=0,
解得:a=-![]() ,
,
∴![]() 时y关于x的函数关系式为y=-
时y关于x的函数关系式为y=-![]() (x-400)2+80000=-
(x-400)2+80000=-![]() x2+400x.
x2+400x.
∵当x>400时,点A后面的部分与x轴平行,
∴x>400时y关于x的函数关系式为y=80000.
∴y关于x的函数关系式为:y=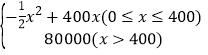 .
.
(2)∵月纯利润=总销售额-月初投资-产品成本,
∴z=y-25000-100x,
当0≤x≤400时,z=-![]() x2+400x-25000-100x=-
x2+400x-25000-100x=-![]() x2+300x-25000,
x2+300x-25000,
当x>400时,z=80000-25000-100x=-100x+55000,
∴z关于x的函数关系式为z=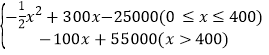
(3)当x>400时,z<-100×400+55000=15000(元);
当0≤x≤400时,z=-![]() x2+300x-25000=-
x2+300x-25000=-![]() (x-300)2+20000.
(x-300)2+20000.
所以,当x=300时,z最大=20000(元).
答:当月产量为300台时,利润最大,最大利润为20000元.

【题目】2007年上海国际汽车展期间,某公司对参观本次车展盛会的且有购车意向的消费者进行了随机问卷调查,共发放900份调查问卷,并收回有效问卷750份.工作人员对有效调查问卷作了统计,其中:
①将消费者年收入的情况整理后,制成表格如下:
年收入(万元) | 4.8 | 6 | 7.2 | 9 | 10 |
被调查的消费者人数(人) | 150 | 338 | 160 | 60 | 42 |
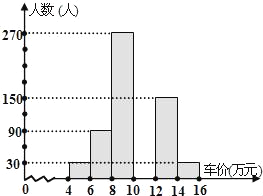
②将消费者打算购买小车的情况整理后,绘制出频数分布直方图(如图,尚未绘完整).(注:每组包含最小值不包含最大值.)请你根据以上信息,回答下列问题:
(1)根据①中信息可知,被调查消费者的年收入的中位数是______万元.
(2)请在图中补全这个频数分布直方图.
(3)打算购买价格10万元以下(不含10万元)小车的消费者人数占被调查消费者人数的百分比是_______.
(4)本次调查的结果,是否能够代表全市所有居民的年收入情况和购车意向?为什么?