题目内容
【题目】综合与实践![]() 四边形旋转中的数学
四边形旋转中的数学
“智慧”数学小组在课外数学活动中研究了一个问题,请帮他们解答.
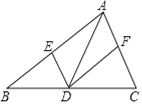
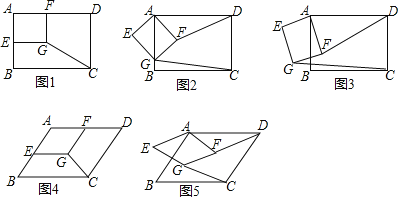
任务一:如图1,在矩形ABCD中,![]() ,
,![]() ,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
![]() 请直接写出CG的长是______.
请直接写出CG的长是______.
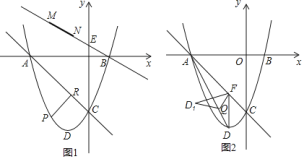
![]() 如图2,当矩形AEGF绕点A旋转
如图2,当矩形AEGF绕点A旋转![]() 比如顺时针旋转
比如顺时针旋转![]() 至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.
至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.
![]() 当矩形AEGF绕点A旋转至如图3的位置时,
当矩形AEGF绕点A旋转至如图3的位置时,![]() 中DF与CG之间的数量关系是否还成立?请说明理由.
中DF与CG之间的数量关系是否还成立?请说明理由.
任务二:“智慧”数学小组对图形的旋转进行了拓展研究,如图4,在ABCD中,![]() ,
,![]() ,
,![]() ,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接
,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接![]() “智慧”数学小组发现DF与CG仍然存在着特定的数量关系.
“智慧”数学小组发现DF与CG仍然存在着特定的数量关系.
![]() 如图5,当AEGF绕点A旋转
如图5,当AEGF绕点A旋转![]() 比如顺时针旋转
比如顺时针旋转![]() ,其他条件不变时,“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系
,其他条件不变时,“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系![]() 请你直接写出这个特定的数量关系.
请你直接写出这个特定的数量关系.
【答案】(1)5;(2)![]() .(3)成立,详见解析.(4)
.(3)成立,详见解析.(4)![]() .
.
【解析】
![]() 延长EG交CD于H,则四边形FGHD是矩形
延长EG交CD于H,则四边形FGHD是矩形![]() 在
在![]() 中,利用勾股定理即可解决问题;
中,利用勾股定理即可解决问题;
![]() 作
作![]() 于
于![]() 利用勾股定理相似三角形的性质,分别求出CG、DF即可解决问题;
利用勾股定理相似三角形的性质,分别求出CG、DF即可解决问题;
![]() 连接AG、
连接AG、![]() 只要证明
只要证明![]() ∽
∽![]() ,可得
,可得![]() 即可解决问题;
即可解决问题;
![]() 通过计算即可解决问题.
通过计算即可解决问题.
![]() 如图1中,延长EG交CD于H,则四边形FGHD是矩形.
如图1中,延长EG交CD于H,则四边形FGHD是矩形.
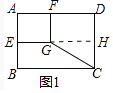
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
故答案为5.
![]() 如图2中,作
如图2中,作![]() 于P.
于P.
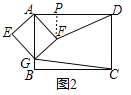
在矩形AEGF中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
由![]() ∽
∽![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() .
.
![]() 成立
成立![]() 理由如下:连接AG、AC.
理由如下:连接AG、AC.
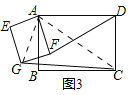
由旋转可知:![]() ,
,
由勾股定理可知:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() .
.
![]() 如图4中,延长EG交CD于H,作
如图4中,延长EG交CD于H,作![]() 于K.
于K.
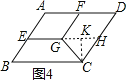
由题意可知四边形FGHD是平行四边形,四边形AEGF是平行四边形,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() .
.
在图5中,连接AG、![]() 同法可证:
同法可证:![]() ∽
∽![]() ,可得:
,可得:![]() ,可得
,可得![]() .
.

 科学实验活动册系列答案
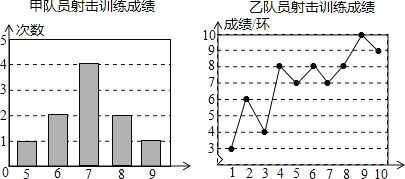
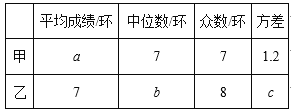
科学实验活动册系列答案【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如表:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 | a | 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
(1)经计算甲和乙的平均成绩是8(环),请求出表中的a= ;
(2)甲成绩的中位数是 环,乙成绩的众数是 环;
(3)若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?