题目内容
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
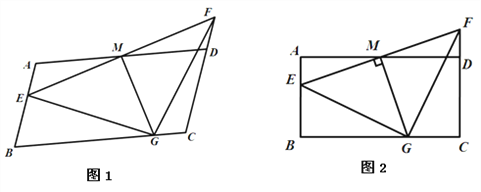
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
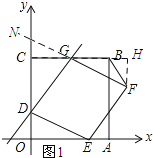
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.

【答案】(1)m=2证明见解析(2)①2;6﹣a(3)m=![]()
【解析】试题分析:(1)将x=0代入y=mx+2得y=2,故此点D的坐标为(0,2),由CG=OD=2可知点G的坐标为(2,6),将点G(2,6)代入y=mx+2可求得m=2;
(2)如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.先证明Rt△GHF≌Rt△EOD,从而得到FH=DO=2,由三角形的面积公式可知:S=6-a.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.由菱形的性质可知:DM⊥GM,点M为DF的中点,根据角平分线的性质可知:MD=CD=4,由中点坐标公式可知点M的纵坐标为3,于是得到ND=1,根据勾股定理可求得MN=![]() ,于是得到点M的坐标为(
,于是得到点M的坐标为(![]() ,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=
,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=![]() .
.
解:(1)∵将x=0代入y=mx+2得;y=2,∴点D的坐标为(0,2).
∵CG=OD=2,∴点G的坐标为(2,6).
将点G(2,6)代入y=mx+2得:2m+2=6.解得:m=2.
证明△DOE≌△GCD(HL),再证明∠GDE=90°,即可证出菱形GDEF为正方形.
(2)①如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.
∵四边形DEFG为菱形,∴GF=DE,GF∥DE.∴∠GNC=∠EDO.
∴∠NGC=∠DEO.∴∠HGF=∠DEO.
在Rt△GHF和Rt△EOD中,
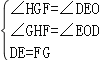 ,
,
∴Rt△GHF≌Rt△EOD.∴FH=DO=2.
∴![]() =
=![]() ×2×(6﹣a)=6﹣a.
×2×(6﹣a)=6﹣a.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.
又∵四边形DEFG为菱形,
∴DM⊥GM,点M为DF的中点.
 ∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∴MD=CD=4.
∵由(2)可知点F的坐标为4,点D的纵坐标为2,
∴点M的纵坐标为3.
∴ND=1.
在Rt△DNM中,MN=![]() =
=![]() .
.
∴点M的坐标为(![]() ,3).
,3).
设直线DM的解析式为y=kx+2.将(![]() ,3)代入得:
,3)代入得:![]() k+2=3.
k+2=3.
解得:k=![]() .
.
∴设直线MG的解析式为y=![]() x+b.将(
x+b.将(![]() ,3)代入得:﹣15+b=3.
,3)代入得:﹣15+b=3.
解得:b=18.
∴直线MG的解析式为y=﹣![]() x+18.
x+18.
将y=6代入得:![]() .
.
解得:x=![]() .
.
∴点G的坐标为(![]() ,6).
,6).
将(![]() ,6)代入y=mx+2得:
,6)代入y=mx+2得:![]() m+2=6.
m+2=6.
解得:m=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案