��Ŀ����
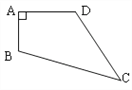
����Ŀ����ͼ�٣�ֱ��y=![]() x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
��1����������F1����ʾ�Ķ��κ����ı���ʽ��
��2������M��������F1λ�ڵڶ�����ͼ���ϵ�һ�㣬���ı���MAOC�͡�BOC������ֱ�ΪS�ı���MAOC��S��BOC����S=S�ı���MAOC��S��BOC����S���ʱ��M�����꼰S�����ֵ��
��3����ͼ�ڣ���������F1��y�ᷭ�۲������ơ��õ�������F2����A��B�루2��������ĵ�M�Ķ�Ӧ��ֱ�ΪA�䡢B�䡢M�䣬����M����M��E��x���ڵ�E����ֱ��A��C�ڵ�D����x�����Ƿ���ڵ�P��ʹ����A�䡢D��PΪ��������������AB��C���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡�(1)y=��![]() x2��
x2��![]() x+4;(2)S�����ֵΪ
x+4;(2)S�����ֵΪ![]() ����ʱ��M����
����ʱ��M����![]() ��5������P������Ϊ��2��0������
��5������P��������2��0������![]() ��0����
��0����
��������
�����������1������һ�κ����Ľ���ʽy=![]() x+4�������A��C�����꣬�ٰ�A��B��C��������룬���ô���ϵ��������κ����Ľ���ʽ����2������M��������F1�ϣ����Կ���M��a����
x+4�������A��C�����꣬�ٰ�A��B��C��������룬���ô���ϵ��������κ����Ľ���ʽ����2������M��������F1�ϣ����Կ���M��a����![]() a2��
a2��![]() a+4�����ֱ����S�ı���MAOC��S��BOC������M��MD��x���ڵ�D����S�ı���MAOC��ֵ������ADM�����������DOCM�����֮�ͣ����S�ı���MAOC��ֵ������S=S�ı���MAOC��S��BOC��ʾ��S��a�Ķ��κ�����ϵ�����ݶ��κ��������ʼ��ɵ�S���ʱ��M�����꼰S�����ֵ����3�����ڲ�ȷ����P�ľ���λ�ã�������Ҫ����P��λ�ý��з������ۣ�����P��A�����ұ�ʱ��������Dz����ڣ�����P��A�������ʱ����ʱ��DA��P=��CAB��������A����D��PΪ���������������AB��C���ƣ����Ϊ������������������ۣ���
a+4�����ֱ����S�ı���MAOC��S��BOC������M��MD��x���ڵ�D����S�ı���MAOC��ֵ������ADM�����������DOCM�����֮�ͣ����S�ı���MAOC��ֵ������S=S�ı���MAOC��S��BOC��ʾ��S��a�Ķ��κ�����ϵ�����ݶ��κ��������ʼ��ɵ�S���ʱ��M�����꼰S�����ֵ����3�����ڲ�ȷ����P�ľ���λ�ã�������Ҫ����P��λ�ý��з������ۣ�����P��A�����ұ�ʱ��������Dz����ڣ�����P��A�������ʱ����ʱ��DA��P=��CAB��������A����D��PΪ���������������AB��C���ƣ����Ϊ������������������ۣ���![]() ����
����![]() ���ֱ���õ�P�����꼴��.
���ֱ���õ�P�����꼴��.
�����������1����y=0����y=![]() x+4��
x+4��
��x=��3��
A����3��0����
��x=0������y=![]() x+4��
x+4��
��y=4��
��C��0��4����
��������F1�Ľ���ʽΪ��y=a��x+3����x��1����
��C��0��4��������ʽ�ã�a=��![]() ��
��
��y=��![]() x2��
x2��![]() x+4��
x+4��
��2����ͼ�������M��a����![]() a2��
a2��![]() a+4��
a+4��
������3��a��0
��B��1��0����C��0��4����
��OB=1��OC=4
��S��BOC=![]() OBOC=2��
OBOC=2��
����M��MD��x���ڵ�D��
��MD=��![]() a2��
a2��![]() a+4��AD=a+3��OD=��a��
a+4��AD=a+3��OD=��a��
��S�ı���MAOC=![]() ADMD+
ADMD+![]() ��MD+OC��OD
��MD+OC��OD
=![]() ADMD+
ADMD+![]() ODMD+
ODMD+![]() ODOC
ODOC
=![]() +
+![]()
=![]() +
+![]()
=![]() ��3����
��3����![]() a2��
a2��![]() a+4��+
a+4��+![]() ��4������a��
��4������a��
=��2a2��6a+6
��S=S�ı���MAOC��S��BOC
=����2a2��6a+6����2
=��2a2��6a+4
=��2��a+![]() ��2+
��2+![]()
����a=��![]() ʱ��
ʱ��
S�����ֵ�����ֵΪ![]()
��ʱ��M����![]() ��5����
��5����
��3����ͼ����������֪��M����![]() ����B������1��0����A����3��0��
����B������1��0����A����3��0��
��AB��=2
��ֱ��A��C�Ľ���ʽΪ��y=kx+b��
��A����3��0����C��0��4������y=kx+b��
�ã�![]() ��
��
��
��y=��![]() x+4��
x+4��
��x=![]() ����y=��
����y=��![]() x+4��
x+4��
��y=2
��![]()
�ɹ��ɶ����ֱ����ã�AC=5��DA��=![]()
��P��m��0��
��m��3ʱ��
��ʱ��P��A������ߣ�
���DA��P=��CAB����
��![]() =
=![]() ʱ����DA��P�ס�CAB����
ʱ����DA��P�ס�CAB����
��ʱ��![]() =
=![]() ��3��m����
��3��m����
��ã�m=2��
��P��2��0��
��![]() =
=![]() ʱ����DA��P�ס�B��AC��
ʱ����DA��P�ס�B��AC��
��ʱ��![]() =
=![]() ��3��m��
��3��m��
m=��![]() ��
��
��P����![]() ��0��
��0��
��m��3ʱ��
��ʱ����P��A���ұߣ�
������CB��O�١�DA��E��
���AB��C�١�DA��P
�����������DA��P����B��AC�������ƣ�
��������������A����D��PΪ���������������AB��C����ʱ����P������Ϊ��2��0������![]() ��0����
��0����