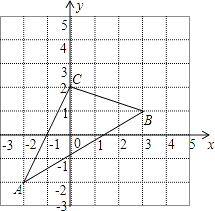题目内容
【题目】如图，在平面直角坐标系中，已知矩形OABC的两个顶点A、B 的坐标分别A（ 
，0）、B（ ，2），∠CAO=30°．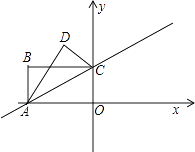
（1）求对角线AC所在的直线的函数表达式；
（2）把矩形OABC以AC所在的直线为对称轴翻折，点O落在平面上的点D处，求点D的坐标；
（3）在平面内是否存在点P，使得以A、O、D、P为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】
（1）
解：由题意得，OA=2 
，∠CAO=30°，
则OC=OAtan∠CAO=2，
即点C的坐标为（0，2），
设直线AC的解析式为：y=kx+b，将点A及点C的坐标代入得： 
，
解得：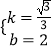 
，
故直线AC的函数表达式为：y= 
x+2
（2）
解：过点D作DE⊥OA于点E，
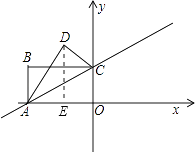
∵∠CAO=30°，
∴∠DAE=60°，
又∵AD=AO=2 ，
∴DE=3，AE= ，
∴OE= ，
故点D的坐标为（﹣ ，3）
（3）
解：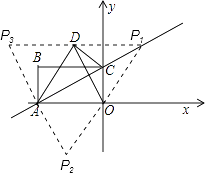 
①当AD为平行四边形的一边时，点P的位置有两个，分别为P1、P2，
当点P位于P1位置时，DP1=AO，
此时可得点P的坐标为（ ，3）；
当点P位于P2位置时，
∵OD=AD，△AOD是等边三角形，
∴点P2与点D关于x轴对称，
此时可得点P的坐标为（﹣ ，﹣3）；
②当AD为平行四年行的对角线时，点P的位置有一个，在P3的位置，
此时DP3=AO，
故可得点P的坐标为（﹣3 ，3）．
综上可得存在点P的坐标，使得以A、O、D、P为顶点的四边形为平行四边形，点P的坐标为（ ，3）或（﹣ ，﹣3）或（﹣3 ，3）
【解析】（1）求出点C的坐标，利用待定系数法即可求出直线AC的函数表达式；（2）过点D作DE⊥OA于点E，利用三角函数的知识，求出DE及OE的长度，即可得出点D的坐标．（3）找到点P的可能位置，利用平行四边形对边相等的性质即可得出点P的坐标．
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能正确解答此题．
