题目内容
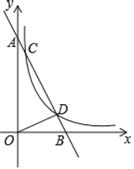
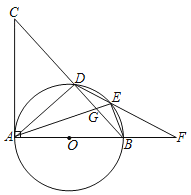
【题目】如图,AB是⊙O的直径,AC⊥AB,BC交⊙O于点D,点E在劣弧BD上,DE的延长线交AB的延长线于点F,连接AE交BD于点G.
(1)求证:∠AED=∠CAD;
(2)若点E是劣弧BD的中点,求证:ED2=EGEA;
(3)在(2)的条件下,若BO=BF,DE=2,求EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)4.
【解析】
(1)可得∠ADB=90°,证得∠ABD=∠CAD,∠AED=∠ABD,则结论得证;
(2)证得∠EDB=∠DAE,证明△EDG∽△EAD,可得比例线段![]() ,则结论得证;
,则结论得证;
(3)连接OE,证明OE∥AD,则可得比例线段![]() ,则EF可求出.
,则EF可求出.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°
∵AC⊥AB,
∴∠CAB=90°,
∴∠CAD+∠BAD=90°
∴∠ABD=∠CAD,
∵![]() =
=![]() ,
,
∴∠AED=∠ABD,
∴∠AED=∠CAD;
(2)证明:∵点E是劣弧BD的中点,
∴![]() ,
,
∴∠EDB=∠DAE,
∵∠DEG=∠AED,
∴△EDG∽△EAD,
∴![]() ,
,
∴ED2=EGEA;
(3)解:连接OE,
∵点E是劣弧BD的中点,
∴∠DAE=∠EAB,
∵OA=OE,
∴∠OAE=∠AEO,
∴∠AEO=∠DAE,
∴OE∥AD,
∴![]() ,
,
∵BO=BF=OA,DE=2,
∴![]() ,
,
∴EF=4.

练习册系列答案
相关题目