题目内容
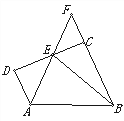
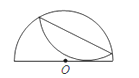
【题目】一张半径为2的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,O为半圆圆心,如果切点分直径之比为3:1,则折痕长为( )
A. 3 B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】C
【解析】
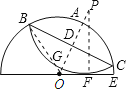
过O作弦BC的垂线OP,垂足为D,分别与弧的交点为A、G,过切点F作PF⊥半径OE交OP于P点,根据垂径定理及其推论得到BD=DC,即OP为BC的中垂线,OP必过弧BGC所在圆的圆心,再根据切线的性质得到PF必过弧BGC所在圆的圆心,则点P为弧BGC所在圆的圆心,根据折叠的性质有⊙P为半径等于⊙O的半径,即PF=PG=OE=2,并且AD=GD,由F点分⊙O的直径为3:1两部分可计算出OF=1,在Rt△OPF中,设OG=x,利用勾股定理可计算出x,则由AG=PG-AP计算出AG,可得到DG的长,于是可计算出OD的长,在Rt△OBD中,利用勾股定理计算BD,即可得到BC的长.
过O作弦BC的垂线OP,垂足为D,分别与弧的交点为A、G,过切点F作PF⊥半径OE交OP于P点,如图,
∵OP⊥BC,
∴BD=DC,即OP为BC的中垂线,
∴OP必过弧BGC所在圆的圆心,
又∵OE为弧BGC所在圆的切线,PF⊥OE,
∴PF必过弧BGC所在圆的圆心,
∴点P为弧BGC所在圆的圆心,
∵弧BAC沿BC折叠得到弧BGC,
∴⊙P为半径等于⊙O的半径,即PF=PG=OE=2,并且AD=GD,
∴OG=AP,
而F点分⊙O的直径为3:1两部分,
∴OF=1,
在Rt△OPF中,设OG=x,则OP=x+2,
∴OP2=OF2+PF2,即(x+2)2=12+22,解得x=![]() -2,
-2,
∴AG=2-(![]() -2)=4-
-2)=4-![]() ,
,
∴DG=![]() ,
,
∴OD=OG+DG=![]() -2+2-
-2+2-![]() =
=![]() ,
,
在Rt△OBD中,BD2=OB2+OD2,即BD2=22-(![]() )2,
)2,
∴BD=![]() ,
,
∴BC=2BD=![]() .
.
故选C.