Question

【题目】已知，在Rt△ABC中，∠ACB＝90°，BC＝4，AB＝4，点D是AC边上的一个动点，将△ABD沿BD所在直线折叠，使点A落在P处．

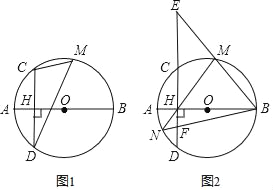
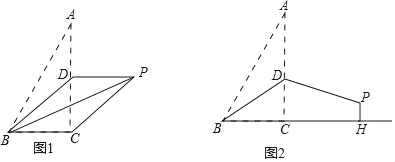
（1）如图1，若点D是AC中点，连接PC．

①求AC的长；

②试猜想四边形BCPD的形状，并加以证明；

（2）如图2，若BD＝AD，过点P作PH⊥BC交BC的延长线于点H，求CH的长．

Answer 1

【答案】（1）①AC＝8，②四边形BCPD是平行四边形．理由见解析；（2）CH＝．

【解析】

（1）①根据勾股定理求出AC即可；

②想办法证明DP∥BC，DP=BC即可；

（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．设BD=AD=x，则CD=8-x，在Rt△BDC中，可得x2=（8-x）2+42，推出x=5，由△ADN∽△ABC，可得，可得推出BN=AN=2，在Rt△BDN中，DN=，由△BDN∽△BAM，可得，可得，推出AM=4，推出AP=2AM=8，由△ADM∽△APE，可得，可得，推出AE=，推出PE=，即可解决问题；

（1）①在Rt△ABC中，∵BC＝4，AB＝4，

∴AC＝＝8，

②如图1中，四边形BCPD是平行四边形．

理由：∵AC＝8，AD＝DC，

∴DC＝AD＝4，

∵BC＝4，

∴BC＝CD＝4，

∴△BCD是等腰直角三角形，

∴∠BDC＝45°，

∴∠ADB＝∠BDP＝135°，

∴∠PDC＝135°﹣45°＝90°，

∴∠BCD＝∠PDC＝90°，

∴DP∥BC，∵PD＝AD＝BC＝2，

∴四边形BCPD是平行四边形．

（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．

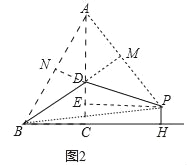
设BD＝AD＝x，则CD＝8﹣x，

在Rt△BDC中，∵BD2＝CD2+BC2，

∴x2＝（8﹣x）2+42，

∴x＝5，

∵DB＝DA，DN⊥AB，

由△ADN∽△ABC，可得，

∴

∴BN＝AN＝2，

在Rt△BDN中，DN＝，

由△BDN∽△BAM，可得，

∴，

∴AM＝4，

∴AP＝2AM＝8，

由△ADM∽△APE，可得，

∴，

∴AE＝，

∴PE＝

易证四边形PECH是矩形，

∴CH＝PE＝．