题目内容
已知：如图，等腰△ABC中，AB＝BC，AE⊥BC于E，EF⊥AB于F，若CE＝2，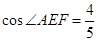
，求EF的长．
解：∵AE⊥BC，EF⊥AB，
∴∠1＋∠2＝90°，∠B＋∠2＝90°．
∴∠1＝∠B．
∴
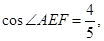
∴Rt△ABE中，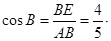
设BE＝4k，则AB＝BC＝5k，EC＝BC－BE＝k＝2．
∴BE＝8．
∴Rt△BEF中，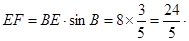
解析
练习册系列答案
相关题目
题目内容
已知：如图，等腰△ABC中，AB＝BC，AE⊥BC于E，EF⊥AB于F，若CE＝2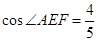，，求EF的长．
解：∵AE⊥BC，EF⊥AB，
∴∠1＋∠2＝90°，∠B＋∠2＝90°．
∴∠1＝∠B．
∴
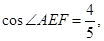
∴Rt△ABE中，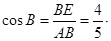
设BE＝4k，则AB＝BC＝5k，EC＝BC－BE＝k＝2．
∴BE＝8．
∴Rt△BEF中，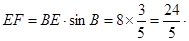
解析
已知：如图，等腰梯形ABCD中，AB∥CD，对角线AC⊥BD于O，BC=13
8、已知：如图，等腰直角三角形ABC中，∠ACB=90°，直线l经过点C，AD⊥l，BE⊥l，垂足分别为D，E．
24、已知：如图，等腰梯形ABCD中，AD∥BC，BD平分∠ABC．
7、已知：如图，等腰△ABC中，AB=AC，AD⊥BC于D，CG∥AB，BG分别交AD、AC于E、F．求证：BE2=EF•EG．
已知：如图，等腰△ABC中，AB=BC，AE⊥BC于E，EF⊥AB于F，cos∠AEF=