题目内容
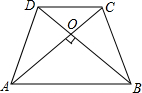 已知:如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13
已知:如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13| 2 |
求:a、b的值.
分析:过C作CE∥DB交AB的延长线于E,作CF⊥AE,从而构建了平行四边形DCEB,则把AB+CD转化到AE边上,然后利用等腰直角三角形的性质求解.
解答: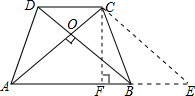 解:过C作CE∥DB交AB的延长线于E,作CF⊥AE
解:过C作CE∥DB交AB的延长线于E,作CF⊥AE
∵BD⊥AC
∴CE⊥AC(2分)
∵ABCD是等腰梯形
∴AC=BD
∵AB∥CD
∴DBEC是平行四边形
∴BE=CD
∴AE=AB+BE=AB+CD=34(4分)
∵CE⊥ACAC=BD=CE
∴△ACE是等腰直角三角形
∴△ACF、△ECF是等腰直角三角形
∴CF=AF=EF=
×34=17(6分)
在RT△CBF中BF=
=
=7
又BF=
(AB-CD)=7
∴AB-CD=14
∵AB+CD=34
∴AB=24CD=10
即a=24、b=10(8分)
 解:过C作CE∥DB交AB的延长线于E,作CF⊥AE
解:过C作CE∥DB交AB的延长线于E,作CF⊥AE∵BD⊥AC
∴CE⊥AC(2分)
∵ABCD是等腰梯形
∴AC=BD
∵AB∥CD
∴DBEC是平行四边形
∴BE=CD
∴AE=AB+BE=AB+CD=34(4分)
∵CE⊥ACAC=BD=CE
∴△ACE是等腰直角三角形
∴△ACF、△ECF是等腰直角三角形
∴CF=AF=EF=
| 1 |
| 2 |
在RT△CBF中BF=
| BC2-CF2 |
(13
|
又BF=
| 1 |
| 2 |
∴AB-CD=14
∵AB+CD=34
∴AB=24CD=10
即a=24、b=10(8分)
点评:本题主要考查等腰梯形的性质的应用.解题关键是作辅助线,这是等腰梯形中常见的一种作法,要熟练掌握.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
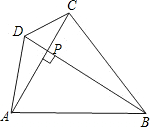
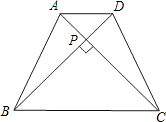
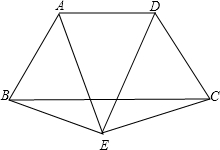 已知:如图,等腰梯形ABCD中,AB=CD,AD∥BC,E是梯形外一点,且EA=ED,求证:EB=EC.
已知:如图,等腰梯形ABCD中,AB=CD,AD∥BC,E是梯形外一点,且EA=ED,求证:EB=EC.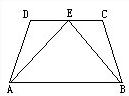 20、已知:如图,等腰梯形ABCD中,AB∥DC,E为DC的中点,求证:∠EAB=∠EBA.
20、已知:如图,等腰梯形ABCD中,AB∥DC,E为DC的中点,求证:∠EAB=∠EBA. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 已知,如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13
已知,如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13