题目内容
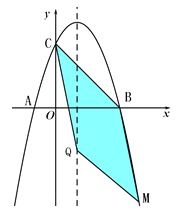
【题目】如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
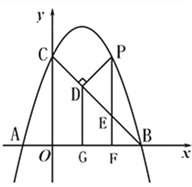
(2)设抛物线上的一个动点P的横坐标为t(0<t<3),过点P作PD⊥BC于点D. ① 求线段PD的长的最大值;② 当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.

【答案】(1) y=-x2+2x+3;(2)①![]() ;②2;(3) (2,3)或(4,-5)或(-2,-5).
;②2;(3) (2,3)或(4,-5)或(-2,-5).
【解析】试题分析: (1)将A、B、C三点的坐标代入y=a(x+1)(x-3)即可求出抛物线的解析式.
(2)①过点P作PE⊥x轴于点E,交BC于点F,求出△PBC的最大面积,即可求出PD的最大值.
②过点D作DG⊥x轴于点G,由于DG∥OC,从而可知![]() ,从而可求出t的值.
,从而可求出t的值.
(3)由于BC是B、C、Q、M为顶点的四边形中的一条固定的线段,因此将此线段分为平行四边形的边和对角线进行讨论即可求出M的坐标.
试题解析:
(1)设抛物线所对应的函数关系式为![]()
将A(-1,0),B(3,0),C(0,3)代入![]() 得:
得:
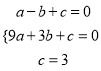
解得: 
∴抛物线所对应的函数关系式为![]()
(2)①设点P的坐标为(t, ![]() )
)
过P作PN⊥x轴于点F,交BC于点E
设直线BC解析式为y=kx+b
把B(3,0),C(0,3)代入y=kx+b得
![]() 解得:k=-1,b=3
解得:k=-1,b=3
∴直线BC解析式为y=-x+3
∴点E坐标为(t, ![]() )
)
PE=![]() -(
-(![]() )=
)=![]()
∵OB=OC=3,∴∠OBC=45°
∵PD⊥BC
∴∠PED=45°
∴PD=PE×sin45°=![]() PE=
PE=![]() (
(![]() )=-
)=-![]()
![]()
![]()
∴当t=![]() 时,PD的最大面积为
时,PD的最大面积为![]()
②过D作DG⊥x轴于点G,则DG∥OC
∴△BOC∽△BGD
∴![]()
当BD=2CD时,BD:BC=2:3
![]()
∴DG=2,即点D的纵坐标为2
把y=2代入y=-x+3得x=1
∴D点坐标为(1,2)
设直线PD解析式为:y=x+b
把D(1,2)代入上式得:
2=1+b,
解得:b=1
∴直线PD解析式为y=x+1
解方程组![]() 得:
得: ![]() ,
, ![]() ( 舍去)
( 舍去)
∴当BD=2CD时,t的值为2
{或∵△PDE是等腰直角三角形,∴![]() )
)
即![]() ,
,
解得: ![]() ,
, ![]() ( 舍去)}
( 舍去)}
(3)∵点Q是抛物线![]() 的对称轴x=1上的动点,
的对称轴x=1上的动点,
∴点Q的横坐标为1,
∵点M在抛物线![]() 上,∴设点M的坐标为(m,
上,∴设点M的坐标为(m, ![]() )
)
(I)如图,当BC、QM为平行四边形的对角线时,
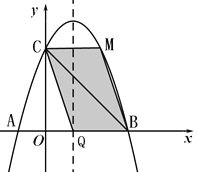
可得: ![]()
即:3=1+m,
∴m=2
∴点M坐标为(2,3)
(II)如图,当BQ、MC为平行四边形的对角线时,
可得: ![]()
即:3+1=m,
∴m=4
∴点M坐标为(4,-5)
(III)如图,当BM、QC为平行四边形的对角线时,

可得: ![]()
即:3+m=1,
∴m=-2
∴点M坐标为(-2,-5)
综合以上所述,满足平行四边形的点M的坐标为(2,3)或(4,-5)或(-2,-5)
点睛: 本题难度较大,考查的是二次函数图象与解析式的灵活运用,一般这样题目都是作为压轴题出现,考生平时应多积累二次函数的综合知识.

 全程金卷系列答案
全程金卷系列答案