题目内容
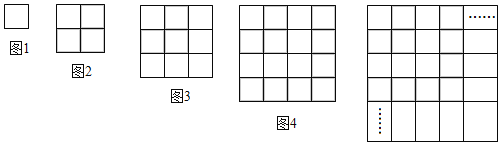
【题目】如图,图1中小正方形的个数为1个;图2中小正方形的个数为:1+3=4=22个;图3中小正方形的个数为:1+3+5=9=32个;图4中小正方形的个数为:1+3+5+7=16=42个;…
(1)根据你的发现,第n个图形中有小正方形:1+3+5+7+…+ = 个.
(2)由(1)的结论,解答下列问题:已知连续奇数的和:(2n+1)+(2n+3)+(2n+5)+……+137+139=3300,求n的值.
【答案】(1)(2n﹣1);n2;(2)n的值为40.
【解析】
(1)根据各图形中小正方形个数的变化可找出变化规律“第n个图形中有小正方形的个数为:1+3+5+7+…+(2n-1)=n2个”,此问得解;
(2)根据(1)的结论结合(2n+1)+(2n+3)+(2n+5)+……+137+139=3300,即可得出关于n的一元二次方程,解之取其正值即可得出结论.
解:(1)∵图1中小正方形的个数为1个;图2中小正方形的个数为:1+3=4=22个;图3中小正方形的个数为:1+3+5=9=32个;图4中小正方形的个数为:1+3+5+7=16=42个;…,
∴第n个图形中有小正方形的个数为:1+3+5+7+…+(2n﹣1)=n2个.
故答案为:(2n﹣1);n2.
(2)∵(2n+1)+(2n+3)+(2n+5)+……+137+139=3300,
∴702﹣n2=3300,
解得:n=40或n=﹣40(舍去).
答:n的值为40.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
【题目】“十·一”黄金周期间,张家界风景区在7天假期中每天旅游人数变化如下表(正号表示人数比前一天多,负号表示比前天少)
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.8 | -0.6 | +0.2 | -0.7 | -1.3 | +0.5 | -2.4 |
(1)若9月30日的旅客人数为![]() 万人,则10月4日的旅客人数为_______万人;
万人,则10月4日的旅客人数为_______万人;
(2)七天中旅客人数最多的一天比最少的一天多______万人;
(3)如果每万人带来的经济收入约为120万元,则黄金周七天的旅游总收入约为多少万元?