Question

如图，在平面直角坐标系中，矩形AOBC的边长为AO=6，AC=8，

（1）如图①，E是OB的中点，将△AOE沿AE折叠后得到△AFE，点F在矩形AOBC内部，延长AF交BC于点G．求点G的坐标；

（2）定义：若以不在同一直线上的三点中的一点为圆心的圆恰好过另外两个点，这样的圆叫做黄金圆．如图②，动点P以每秒2个单位的速度由点C向点A沿线段CA运动，同时点Q以每秒4个单位的速度由点O向点C沿线段OC运动；求：当 PQC三点恰好构成黄金圆时点P的坐标．

 

 

Answer 1

【答案】

（1）(8，)；（2），，． 

【解析】

试题分析：（1）由折叠对称的性质可得DAOE≌DAFE，从而推出DEFG≌DEBG，得到DAOE∽DAEG，因此AE²=AO×AG，在Rt△AOE中，由勾股定理可得AE²=36+16=52，从而得AG=，在Rt△ABM中，由勾股定理可得CG=，从而BG=，得到G的坐标为(8，)；（2）分点C为黄金圆的圆心，点P为黄金圆的圆心，点Q为黄金圆的圆心三种情况讨论即可.

试题解析：（1）如图，连接EG，

由题意得：DAOE≌DAFE，∴ÐEFG=ÐOBC=90⁰.

又∵E是OB的中点，∴EG=EG，EF=EB=4．∴DEFG≌DEBG．

∴ÐFEG=ÐBEG，ÐAOB=ÐAEG=90⁰. ∴DAOE∽DAEG，AE²=AO×AG.

又在Rt△AOE中，∵AO=6，OE=4，∴AE²=36+16=52.

∴52=6×AG，AG=.

在Rt△ABM中，由勾股定理可得CG=，∴BG=．

∴G的坐标为(8，) .

（2）设运动的时间为t秒，

当点C为黄金圆的圆心时，则CQ=CP，

即：2t=10—4t，得到t=，此时CP=，AP=，P点坐标为．

当点P为黄金圆的圆心时，则PC=PQ，

如图①，过点Q作AC的垂线交AC于点E，CQ=10—4t，CP=2t．

由三角形相似可知：EQ=CQ=，PE=，

则，化简得：，

解得 (舍去) ．

此时，AP=，P点坐标为．

当点Q为黄金圆的圆心时，则QC=PQ，

如图②，过点Q作AC的垂线交AC于点F，CQ=10—4t，CP=2t.

由三角形相似可知：QF=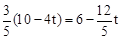，PF=，

则 ，整理得．

解得 (舍去) ．

此时，AP=，P点坐标为．

综上所述，P点坐标为，，．

考点：1. 折叠和双动点问题；2.新定义；3.矩形的性质；4全等三角形的判定和性质；5.相似三角形的判定和性质；6.勾股定理；7.解一元二次方程；8.分类思想的应用.