��Ŀ����
����Ŀ����ͼ������![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ�������˶��ٶȾ�Ϊ
ͬʱ�������˶��ٶȾ�Ϊ![]() ����
����![]() ��
��![]() �˶�������
�˶�������![]() ֹͣ����
ֹͣ����![]() ��
��![]() �˶�������
�˶�������![]() ֹͣ
ֹͣ![]() ������˶�������
������˶�������![]() ֹͣ������
ֹͣ������![]() ��
��![]() ��
��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ������涨���߶������
������涨���߶������![]() �ļ���ͼ�Σ�����
�ļ���ͼ�Σ�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��
��
��ͼ������![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ�������˶��ٶȾ�Ϊ
ͬʱ�������˶��ٶȾ�Ϊ![]() ����
����![]() ��
��![]() �˶�������
�˶�������![]() ֹͣ����
ֹͣ����![]() ��
��![]() �˶�������
�˶�������![]() ֹͣ
ֹͣ![]() ������˶�������
������˶�������![]() ֹͣ������
ֹͣ������![]() ��
��![]() ��
��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ������涨���߶������
������涨���߶������![]() �ļ���ͼ�Σ�����
�ļ���ͼ�Σ�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��
��
![]() ��գ�
��գ�![]() ________
________![]() ��
��![]() ��
��![]() ֮��ľ���Ϊ________
֮��ľ���Ϊ________![]() ��
��
![]() ��
��![]() ʱ����
ʱ����![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
![]() ֱ��д���������˶������У�ʹ
ֱ��д���������˶������У�ʹ![]() ������
������![]() һ��ƽ�е�����
һ��ƽ�е�����![]() ��ֵ��
��ֵ��

���𰸡���1��5��![]()
��������
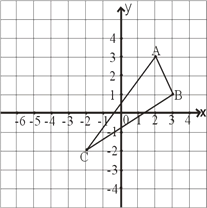
��1�����ݹ��ɶ����������AB�����������ʽ���AB��CD֮��ľ��룮
��2����4��x��10ʱ���˶����̷�Ϊ�����Σ���Ҫ�������ۣ�����©�⣺
�ٵ�4��x��5ʱ�����ͼ1-1��ʾ����ʱ��Q���O�غϣ���P���߶�BC�ϣ�
�ڵ�5��x��9ʱ�����ͼ1-2��ʾ����ʱ��Q���߶�OB�ϣ���P���߶�CD�ϣ�
�۵�9��x��10ʱ�����ͼ1-3��ʾ����ʱ��Q���B�غϣ���P���߶�CD�ϣ�
��3�����������Σ���Ҫ�������ۣ��ֱ���㣺
����PQ��CD�����ͼ2-1��ʾ��
����PQ��BC�����ͼ2-2��ʾ��
�⣺��1��������ABCD�У�AC=6cm��BD=8cm��
��AC��BD��
��AB=![]() =
=![]() =5��
=5��
��AB��CD��ľ���Ϊh��
���ABC�����S=![]() ABh��
ABh��
�֡ߡ�ABC�����S=![]() S����ABCD=
S����ABCD=![]() ��
��![]() ACBD=
ACBD=![]() ��6��8=12��
��6��8=12��
��![]() ABh=12��
ABh=12��
��h=![]() =
=![]() ��
��
��2�����CBD=��CDB=�ȣ����ã�sin��=![]() ��cos��=
��cos��=![]() ��
��
�ٵ�4��x��5ʱ�����ͼ1-1��ʾ����ʱ��Q���O�غϣ���P���߶�BC�ϣ�
��PB=x��
��PC=BC-PB=5-x��
����P��PH��AC�ڵ�H����PH=PCcos��=![]() ��5-x����
��5-x����
��y=S��APQ=![]() QAPH=
QAPH=![]() ��3��
��3��![]() ��5-x��=-
��5-x��=-![]() x+6��
x+6��
�ڵ�5��x��9ʱ�����ͼ1-2��ʾ����ʱ��Q���߶�OB�ϣ���P���߶�CD�ϣ�
PC=x-5��PD=CD-PC=5-��x-5��=10-x��
����P��PH��BD�ڵ�H����PH=PDsin��=![]() ��10-x����
��10-x����
��y=S��APQ=S����ABCD-S��ABQ-S�ı���BCPQ-S��APD
=S����ABCD-S��ABQ-��S��BCD-S��PQD��-S��APD
=![]() ACBD-
ACBD-![]() BQOA-��
BQOA-��![]() BDOC-
BDOC-![]() QDPH��-
QDPH��-![]() PD��h
PD��h
=![]() ��6��8-
��6��8-![]() ��9-x����3-[
��9-x����3-[![]() ��8��3-
��8��3-![]() ��x-1��
��x-1��![]() ��10-x��]-
��10-x��]- ![]() ��10-x����
��10-x����![]()
=-![]() x2+
x2+![]() x-
x-![]() ��
��
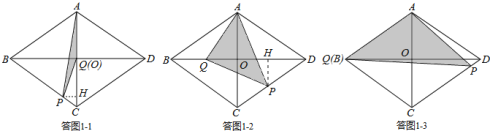
�۵�9��x��10ʱ�����ͼ1-3��ʾ����ʱ��Q���B�غϣ���P���߶�CD�ϣ�
y=S��APQ=![]() AB��h=
AB��h=![]() ��5��
��5��![]() =12��
=12��
������������4��x��10ʱ��y��x֮��ĺ�������ʽΪ��
y=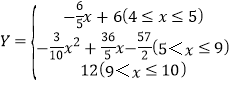 ��
��
��3�������������
����PQ��CD�����ͼ2-1��ʾ��
��ʱBP=QD=x����BQ=8-x��
��PQ��CD��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��x=![]() ��
��
����PQ��BC�����ͼ2-2��ʾ��
��ʱPD=10-x��QD=x-1��
��PQ��BC��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��x=![]() ��
��
��������������������x��ֵΪ![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�