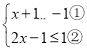题目内容
【题目】如图,矩形ABCD中,AB=5,BC=12,将矩形绕着点D顺时针旋转,当点C落在对角线BD上的点E处时,点A、B分别落在点G、F处,那么AG:BF:CE=_____.
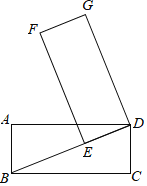
【答案】12:13:5
【解析】
作GH⊥AD于H,CN⊥DE于N,由矩形的性质得出AD=BC=12,AB=CD=5,∠BCD=90°,由旋转得:AD=DG=EF=12,CD=DE=5,∠BEF=90°,由勾股定理得出BF=4![]() ,由三角函数和勾股定理求出AG=
,由三角函数和勾股定理求出AG=![]() ,CE=
,CE=![]() ,即可得出结果.
,即可得出结果.
作GH⊥AD于H,CN⊥DE于N,如图所示:
∵四边形ABCD是矩形,
∴AD=BC=12,AB=CD=5,∠BCD=90°,
由旋转得:AD=DG=EF=12,CD=DE=5,∠BEF=90°,
![]()
![]()
![]() ∵∠GDE=∠CDA=90°,
∵∠GDE=∠CDA=90°,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
同理:CN=CD×sin∠CDB=5×![]() ,
,
![]()
![]() ∴AG:BF:CE=12:13:5;
∴AG:BF:CE=12:13:5;
故答案为:12:13:5.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):

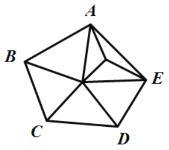
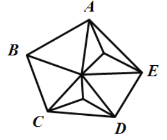
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.