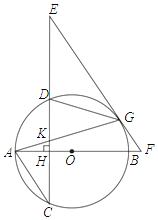题目内容
【题目】△ABC中,∠ACB=90°,tanB=![]() ,AB=5,点O为边AB上一动点,以O为圆心,OB为半径的圆交射线BC于点E,以A为圆心,OB为半径的圆交射线AC于点G.
,AB=5,点O为边AB上一动点,以O为圆心,OB为半径的圆交射线BC于点E,以A为圆心,OB为半径的圆交射线AC于点G.
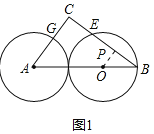
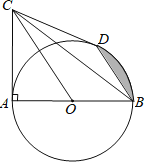
(1)如图1,当点E、G分别在边BC、AC上,且CE=CG时,请判断圆A与圆O的位置关系,并证明你的结论;
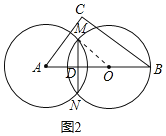
(2)当圆O与圆A存在公共弦MN时(如图2),设OB=x,MN=y,求y关于x的函数解析式,并写出定义域;
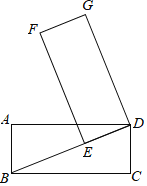
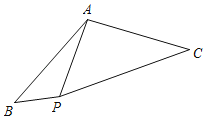
(3)设圆A与边AB的交点为F,联结OE、EF,当△OEF为以OE为腰的等腰三角形时,求圆O的半径长.

【答案】(1)圆A与圆O外切,理由见解析;(2)y=![]() (
(![]() <x<5);(3)当△OEF为以OE为腰的等腰三角形时,圆O的半径长为
<x<5);(3)当△OEF为以OE为腰的等腰三角形时,圆O的半径长为![]() 或
或![]() 或5.
或5.
【解析】
(1)由三角函数得出AC=3,BC=4,作OP⊥BE于P,则PB=PE,OP∥AC,得出![]() =
=![]() ,设PB=PE=x,则CG=CE=4﹣2x,得出OB=
,设PB=PE=x,则CG=CE=4﹣2x,得出OB=![]() x,AG=AC﹣CG=2x﹣1,得出方程,得出x=
x,AG=AC﹣CG=2x﹣1,得出方程,得出x=![]() ,OB═
,OB═![]() ,求出OA=AB﹣OB=2OB,即可得出结论;
,求出OA=AB﹣OB=2OB,即可得出结论;
(2)连接OM,由相交两圆的性质得出OA与MN垂直平分,∠ODM=90°,DM=![]() MN=
MN=![]() y,AD=OD=
y,AD=OD=![]() (5﹣x),由勾股定理得出方程,整理即可;
(5﹣x),由勾股定理得出方程,整理即可;
(3)分三种情况:①当圆O与圆A外切,OE=OF时,圆O与圆A外切,圆O的半径长OB=![]() ;
;
②当OE=FE时,圆O与圆A相交,作EH⊥OF于H,则OF=OH=![]() ﹣OB,证明△BEH∽△BAC,得出EH=
﹣OB,证明△BEH∽△BAC,得出EH=![]() ,在Rt△OEH中,由勾股定理得出方程,解方程即可;
,在Rt△OEH中,由勾股定理得出方程,解方程即可;
③当O与A重合时,OE=OF,OE=AB=5;即可得出结论.
(1)圆A与圆O外切,理由如下:
∵∠ACB=90°,tanB=![]() ,AB=5,∴AC=3,BC=4,
,AB=5,∴AC=3,BC=4,
作OP⊥BE于P,如图1所示:
则PB=PE,OP∥AC,
![]() ,
,
设PB=PE=x,则CG=CE=4﹣2x,
![]()
![]()
![]() 解得:x=
解得:x=![]() ,
,
∴OB═![]() ,
,
∴OA=AB﹣OB=5![]() =2OB,
=2OB,
∴圆A与圆O外切;
(2)连接OM,如图2所示:
∵圆O与圆A存在公共弦MN,
∴OA与MN垂直平分,
∴∠ODM=90°,DM=![]()
由勾股定理得:DM2=OM2﹣OD2,即
整理得:y2=3x2+10x﹣25,
∴y=![]() ;
;
(3)分三种情况:
①当圆O与圆A外切,OE=OF时,圆O与圆A外切,圆O的半径长OB=![]() ;
;
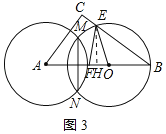
②当OE=FE时,圆O与圆A相交,如图3所示:
作EH⊥OF于H,则OF=OH=![]() ﹣OB,
﹣OB,
∵∠B=∠B,∠EHB=90°=∠C,
∴△BEH∽△BAC,
∴![]() ,
,
∴EH=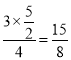 ,
,
在Rt△OEH中,由勾股定理得: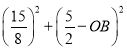 =OE2=OB2,
=OE2=OB2,
解得:OB=![]() ;
;
③当O与A重合时,OE=OF,F与B重合,OE=AB=5;
综上所述,当△OEF为以OE为腰的等腰三角形时,圆O的半径长为![]() 或
或![]() 或5.
或5.