题目内容
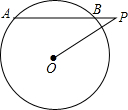（2013•本溪）如图，⊙O的半径是3，点P是弦AB延长线上的一点，连接OP，若OP=4，∠APO=30°，则弦AB的长为（ ）分析：先过O作OC⊥AP，连结OB，根据OP=4，∠APO=30°，求出OC的值，在Rt△BCO中，根据勾股定理求出BC的值，即可求出AB的值．
解答：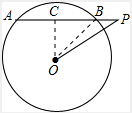
解：过O作OC⊥AP于点C，连结OB，
∵OP=4，∠APO=30°，
∴OC=sin30°×4=2，
∵OB=3，
∴BC=
=
=
，
∴AB=2
；
故选A．
解：过O作OC⊥AP于点C，连结OB，∵OP=4，∠APO=30°，
∴OC=sin30°×4=2，
∵OB=3，
∴BC=
| OB2-OC2 |
| 32-22 |
| 5 |
∴AB=2
| 5 |
故选A．
点评：此题考查了垂经定理，用到的知识点是垂经定理、含30度角的直角三角形、勾股定理，解题的关键是作出辅助线，构造直角三角形．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
（2013•本溪）如图放置的圆柱体的左视图为（ ）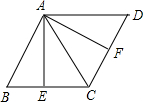
（2013•本溪）如图，在菱形ABCD中，∠BAD=2∠B，E，F分别为BC，CD的中点，连接AE、AC、AF，则图中与△ABE全等的三角形（△ABE除外）有（ ）
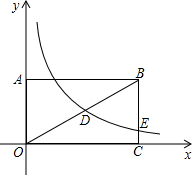（2013•本溪）如图，在矩形OABC中，AB=2BC，点A在y轴的正半轴上，点C在x轴的正半轴上，连接OB，反比例函数y=
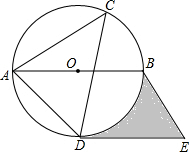（2013•本溪）如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD=45°，⊙O的半径是4cm