题目内容
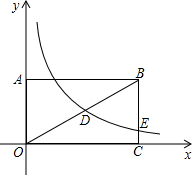（2013•本溪）如图，在矩形OABC中，AB=2BC，点A在y轴的正半轴上，点C在x轴的正半轴上，连接OB，反比例函数y=| k |
| x |
分析：首先根据E点横坐标得出D点横坐标，再利用AB=2BC，得出D点纵坐标，进而得出k的值．
解答：解：∵在矩形OABC中，AB=2BC，反比例函数y=
（k≠0，x＞0）的图象经过OB的中点D，与BC边交于点E，点E的横坐标是4，
∴D点横坐标为：2，AB=OC=4，BC=
AB=2，
∴D点纵坐标为：1，
∴k=xy=1×2=2．
故选：B．
| k |
| x |
∴D点横坐标为：2，AB=OC=4，BC=
| 1 |
| 2 |
∴D点纵坐标为：1，
∴k=xy=1×2=2．
故选：B．
点评：此题主要考查了点的坐标性质以及k与点的坐标性质，得出D点坐标是解题关键．
练习册系列答案
相关题目
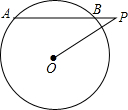（2013•本溪）如图，⊙O的半径是3，点P是弦AB延长线上的一点，连接OP，若OP=4，∠APO=30°，则弦AB的长为（ ）
（2013•本溪）如图放置的圆柱体的左视图为（ ）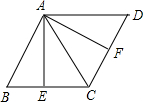
（2013•本溪）如图，在菱形ABCD中，∠BAD=2∠B，E，F分别为BC，CD的中点，连接AE、AC、AF，则图中与△ABE全等的三角形（△ABE除外）有（ ）
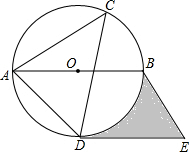（2013•本溪）如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD=45°，⊙O的半径是4cm